GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE

Question One

Part A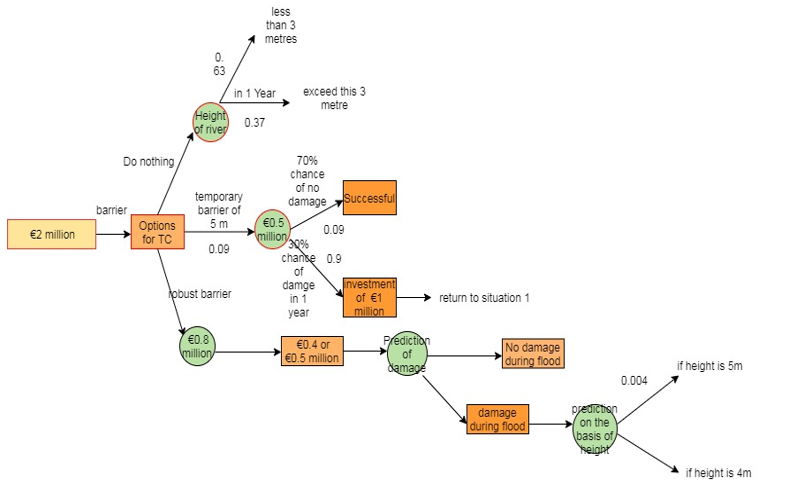GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE

Fig 1: Decision Tree

(Source: draw.io)

Get Assignment Help from Industry Expert Writers (1)

Part B

Optimal Policy for TC

There is the use of the “Markov Decision-making process” which is the most efficient way to judge the situation through the mathematical framework. The Solution within an effective way is the part of the Decision making process in a random way (Adair, 2019).http://GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE

There are a total of three steps, followed by four consecutive steps. States, Model, Action and Reward are the part of the stages of “Markov decision making” process.

States: S

The set of action is defined as,

There is also the implementation of probability which helps to reconsider the particular scenario. Following the probability,

Get Assignment Help from Industry Expert Writers (1)

Model: T(s,a,s’) ~ Pc (s’| s,a)

Actions: A(s),

Reward: R(s), R(s,a), R(s,a,s’)

There is the implementation of the policy on the basis of the above developed criteria.

 Policy: π(s) -> a

The calculation of the π* for the particular decision making process which are needed to be solved on the basis of the particular decision making process (Zamzam et al. 2018).  “Markov decision making” process to follow the algorithm for particular Optimal Policy.

Step 1, Findings of , define the value from n to 0

Step 2, for each, calculate the formula

Here, ]

Step 3, Increase the value of  by 1, back to step 2

There is the calculation of the “Expected Average Cost” for the particular Scenario.

There are a total of three options which are helps in identifying the various options in the identification of the given problem for the particular issue.

In Option 1, T.C. does nothing

Probability for the Particular Context,

If river height exceed from initial to 3 meter

Compensation paid by T.C. for damage in one year € 2 million

So, 2.37

In Option 2, Temporary Barrier constructed T.C.

Probability for the Particular Context,

Initial Investment, € 0.5 million

There is a total of 30% chance of damage for, 1year

So,

In Option 3, Robust Barrier Construction

Initial Interment is, € 0.8 million

Two conditions are needs to follow with respect to the height of the barrier.

Given, Barrier Height = 5m,

Then probability,

Given,

Barrier Height = 4m,

Then probability,

So,

 

Now, calculation of final

So,

 

“Expected Minimized Cost” is the resultant criteria which are used for the minimization of the Solution for the given scenario of risk management in River Scheldt (Han et al. 2018).http://GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE

There is the calculation of the expected minimized cost, which is helpful for findings of the minimized cost in the particular area. Terenure Council needs to follow option two for the further development of flood plains.

Question Two

Part A

In this section, there is a total of two tables which describe the Profit, utility function with the “mean number of passenger” to obtain the advertisement process of “light rail-system in French local authority” (Vilonia and Ganesan, 2018).http://GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE

There is the development of the particular criteria which needs to solve for the further implementation of Optimal Policy. 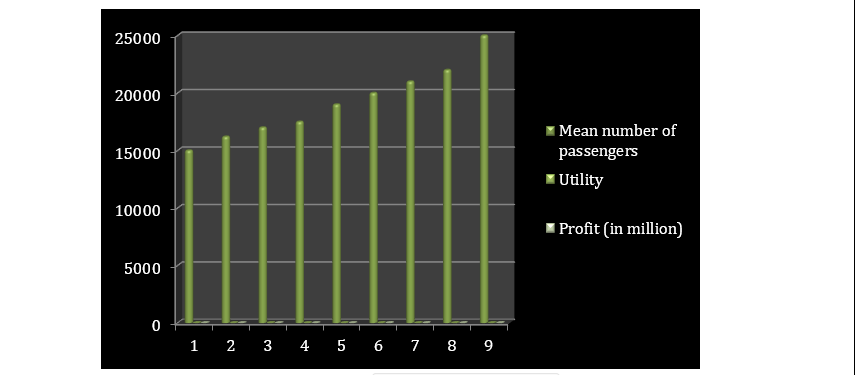GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE 1

Fig 2: Utility function

(Source: Ms Excel)

Part B

  1. I)

There is the development of the utility function according to the “elicitation session”. There is the implementation of utility function as well as the “man number of passenger” which are the part of the particular Solution depending on the “two-variable utility function”.

Here,

According to the given data,  and

i.e.

In the Scenario 1,

Reduction of fare there is the use of the advertisement

Annual profit = € 1 million, So Utility

i.e.

Increment in the “mean number of passenger” = 20000

The probability for the particular scenario,

Then there is increment in the “mean number of passenger” = 14000

Annual profit for the particular scenario = € 3 million

And the for the particular case, Utility,

i.e.

In the Scenario 2,

According to the given scenario if there is the reduction of fare with the use of advertisement

Annual profit = € 1.7 million, So Utility,

So,  , “mean number of passenger” increased, 25000

Annual profit for the particular scenario = € 2 million

And the for the particular case, Utility,

If

There is the “mean number of passenger” increased, 22000

So,

i.e.

In the Scenario 3,

Possibility of developed scenario,

Annual profit = € 1.1 million, So Utility,

The probability of the particular context,  ,

There is the incrimination of the “mean number of passenger”, 25000

Annual profit = € 1.4 million,

So there is the Utility,

If the probability

then there is the increment of “mean number of passenger”, 22000

So,

So,

The entire scenario gives the different value of  for different utility as well as the different probability (Lukan et al. 2018).

So, the need of the developed problem is the part describe accordingly by following “Markov Decision making process”.

“Expected average cost”,

There is the calculation of the particular average cost is the part which emphasis the optimal policy for the development of the given criteria. Most optimal Solution is the part which helps to emphasis the requirement for certain criteria.

There is use of the “Markov decision making process” which helps in the implementation of the particular scenario of using the advertisement by “French Local Authority” (Tuyen, 2018).http://GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE

Use of the decision making process describe the requirement of Scenario 3, which gives the most feasible Solution for the particular problem. There is also the description of utility which helps to describe the ethical part in the implementation of optimal policy.

II)

The Optimal policy for the particular problem gives that there is the implementation of the certain advertisement policy for “French Local Authority”. Among the total three scenarios there is the implementation of the deferment problem which follows the “Markov Decision making process”.

Scenario 3 gives the most feasible optimal policy for the particular context which follows the advertisement process of rail operators. Utility function gives the different Solution for the given problem.

The particular problem is the part which also creates an impact in the implementation of particular scenario. Elicitation is the process which helps in the processing of the data for the development of the optimal policy through particular decision making process.

Question Three    

Maximin rule: In the particular decision making process there is the implementation of rather maximization of loss which gives the better selection of the particular circumstances.

The principal of the particular problem describe that, there is the need of the evolution of particular problem which gives the preferable outcome for the particular scenario.

The maximization of the certain profit with the minimization of the loss is the part which helps to describe the certain data in the particular context of selection of the particular options.

Maximin value = 45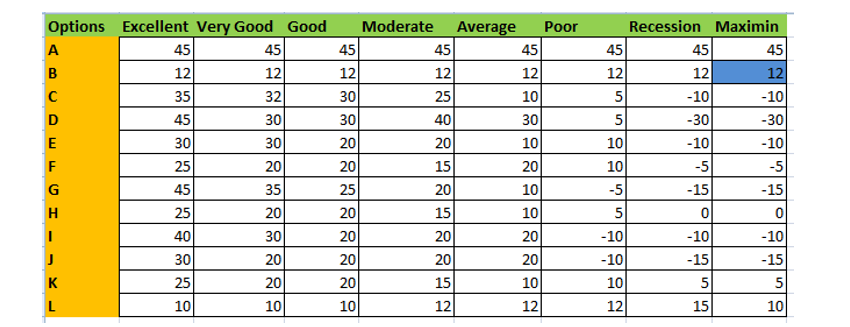GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE 2

Fig 3: Maximin Calculation

(Source: M.S. Excel)

Maximax rule: The Maximax rule or Maximax criterion mainly refers to the decision-making rule in case of uncertainty. This rule has some specifications that mainly conduct the rule process and the calculation of the planning’s and inputs with such balance.

The main rule under this method is to consider the option that has the most and the biggest gain among all the other options (Marshall et al. 2019).http://GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE

With the help of this the action plays the role for the circumstances and the provided circumstances are the instance as, the results must show the best possible look of the inputs and outputs, the decision-making must consider the rule regarding choosing the alternative option with least attractive outcome.

The second rule decides and optimizes that it maximizes the minimum profit of the planning. The decision-making rule mainly is used as the use of this helps in minimizing the regret of making the wrong Decision.

Maximax value = 12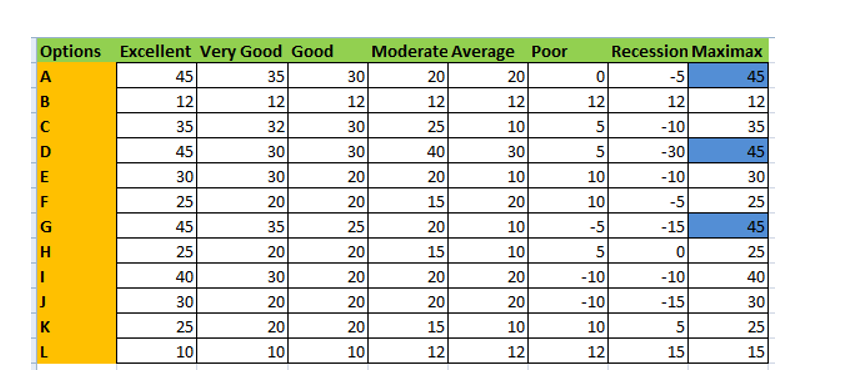GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE 3

 

Fig 3: Maximax Calculation

(Source: M.S. Excel)

ENPV: The calculation of ENPV gives the most feasible Solution for the [particular resulting problem which consider under the formulation of each option selected for the particular criterion. The formula of ENPV is,

“ENPV =  “

Following this formula there is the development of the particular problem which helps in the particular development of ENPV calculation for most preferable scenario (sinews.siam.org, 2020).http://GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE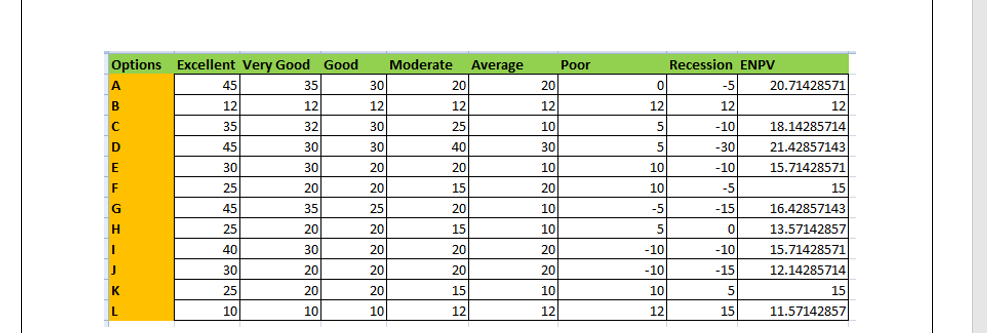GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE 4

Fig 4: ENPV Calculation

(Source: M.S. Excel)

Minimax regret: There is the development of the calculation is based on the matrix developed for the particular criterion according to the implementation of developed criterion.

There is the need of the particular problem which ensures the particular context of the given scenario.  There is the need of the developed problem according to the implementation of the regret matrix using minimax rule. [Referred to Appendix 1]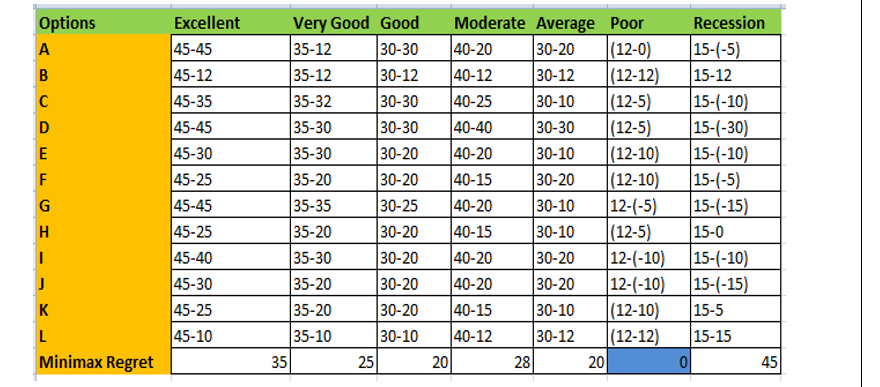GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE 5

Fig 5: Minimax regret Calculation

(Source: M.S. Excel)

Hurwitz rule:

“Weighted Income = [a* most favorable pay-off] + [(1-a)*least favorable pay-off]”

Following this formula there is the implementation of weighted income for the certain condition which also helps full to ensure Hurwitz rule.

There is also the development and the implementation of the favorable income according to the development of certain criteria. The most and least pay-off are the part of development of weighted income.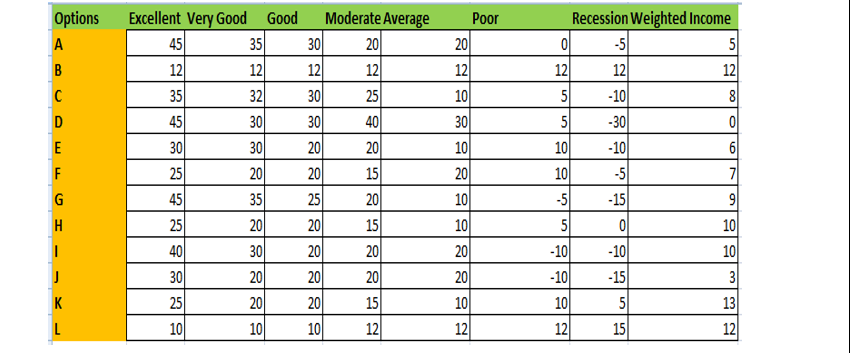GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE 6

Fig 5: Weighted Income Calculation

(Source: M.S. Excel)

 

Part B

There is the calculation of the weighted income which follows the certain condition by following the Hurwitz rule.

Part C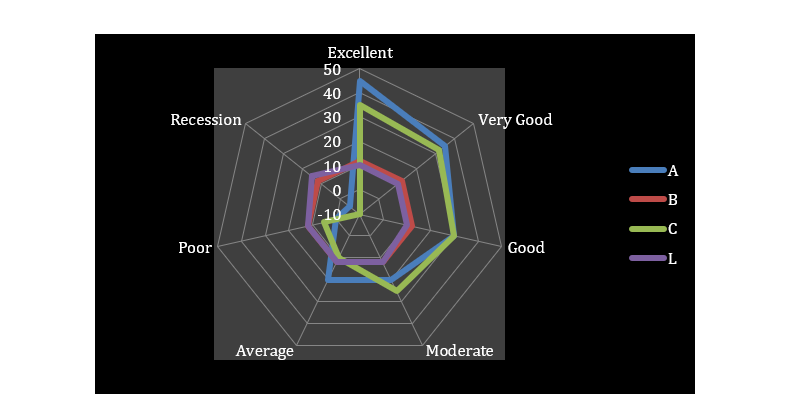GREAT BSV11105 PROJECT RISK MANAGEMENT SAMPLE 7

 

Fig 8: Spider Diagram for A, B, C & L

(Source: MS-Excel)

Reference List

Book

Adair, J., 2019. Decision Making and Problem Solving: Break Through Barriers and Banish Uncertainty at Work.  U.S: Kogan Page Publishers.

Journal

Han, J., Sciaretta, A., Ojeda, L.L., De Nunzio, G. and Thibault, L., 2018. Safe-and eco-driving control for connected and automated electric vehicles using analytical state-constrained optimal Solution. IEEE Transactions on Intelligent Vehicles, 3(2), pp.163-172.

Luján, J.M., Guardiola, C., Pla, B. and Reig, A., 2018. Analytical optimal Solution to the energy management problem in series hybrid electric vehicles. IEEE Transactions on Vehicular Technology, 67(8), pp.6803-6813.

Marshall, J.A., Reina, A. and Bose, T., 2019. Multiscale Modelling Tool: Mathematical modelling of collective behaviour without the maths. PloS one, 14(9).

Tuyen, N.H., 2018. The Process of Approaching and Implementing Experiential Learning for Teaching Maths to Junior Secondary School Students in Viet Nam. American Journal of Educational Research, 6(6), pp.877-882.

Vinoliah, E.M. and Ganesan, K., 2018, April. Fuzzy optimal Solution for a fuzzy assignment problem with octagonal fuzzy numbers. In Journal of Physics: Conference Series (Vol. 1000, No. 1, p. 012016). IOP Publishing.

Zamzam, A.S., Dall’Anese, E., Zhao, C., Taylor, J.A. and Sidiropoulos, N.D., 2018. Optimal Water–Power Flow-Problem: Formulation and Distributed Optimal Solution. IEEE Transactions on Control of Network Systems, 6(1), pp.37-47.

Website

sinews.siam.org, (2020), Decision Making in Mathematics, Available at: https://sinews.siam.org/Details-Page/the-mathematics-of-decision-making-is-there-a-perfect-model [Accessed on: 04.03.2020]

 

 

Appendices

Appendix 1: Regret Matrix

(Source: M.S.- Excel)

 

 

Appendix 2: Utility Function Implementation

(Source: MS-Excel)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Leave a Comment