CE889-7-SU NEURAL NETWORKS & DEEP LEARNING SAMPLE
Question 1:
The pooling layer plays important role in the neural network. The main purpose of this layer is to reduce the spatial size of the image, the image that is reduced by the pooling lawyer is an input image. With the help of this layer, the number of computations is used to reduce the network. The size of the feature maps in the neural network is also reduced with the help of the pooling layer. As the number of access computations is reduced due to this layer when the new computations will make by this network are fast (Aggarwal, C.C., 2018). Due to the access p[arameter there speed of the network is getting slow but with the help of the pooling layer, it is used to reduce the parameters. When the parameters are used with the network it is directly affected by the speed of the network. The speed of the computations is getting faster which is so good for the network. The dimension of the network is obtained with the help of the pooling layer. For obtaining the dimension of the network there is a formula that will help to find the dimension of the neural network. The map dimension is also found with the help of the pooling layer. For obtaining the dimension of the map using the pooling layer there is a formula and a whole calculation. “nh * nw * nc” This is the main formula by which the dimension of the map can be found in the neural network.
“(nh – f + 1) / s x (nw – f + 1)/s x nc
where,
-> nh – the height of the feature map
-> nw – width of the feature map
-> nc – number of channels in the feature map
-> f – size of filter
-> s – stride length”
This is the calculation part for finding the map of the network using the pooling layer.
Question 2: Define the error as: E =, Σ ( y i – log(W ^ 2 x i u))2
Then, ∂ E / ∂ W = Σ – 2 ( y i – log(W ^ 2 x i u)) * 1/W^2xiu * 2 W ^ x i
= Σ – 4 y i – log(W ^ 2 x i u))/W
Now, (W ^ 2 x i u)) = 入Σ * ( y i – log(W ^ 2 x i u))/W
O(k ^ 6): It’s O(# for the basics functions of 3) for solving this equation
And the # of basic function is ½ (K + 1) (K + 2)
O(K ^ 2)
O(K ^ 2) computing the SK takes ½ (k + 1) (K + 2)
O(K ^ 3)
Question 2.1:
2 ^4 = 16
There is a total of 4 possible inputs and for each input, there are 4 possible outputs are there in this calculation.
Question 2.2:
Any booter function can be requested using a combination of AND, NOT, and OR gates. And each of the gates is easily represented us network for example,
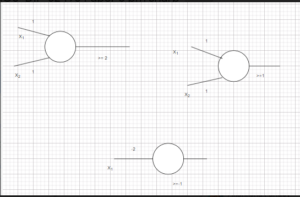
Figure 1: Different gates
(Source: self-creted in draw.io)
Question 2.3:
yes, a play of degree one is just f(X) = a x + b which can be represented using one unit and a linear activation function
Question 2.4:
No, it’s not possible to present x ^ 2.
Question 2.5:
No, not with their actual function you need to be able to multiply 2 inputs.
Question 2.6::
yes,
X1, X2, X3, X4 一🔵 一Y
For X1: (W ^ 2 x i u))
For X2:(W ^ 3 x i u))
For X3: (W ^ 4 x i u))
For X4: (W ^ 5 x i u))
Question 2.7:
yes,
Y = c ^ 2 (W ^ 2 x i u)) X1 + c ^2 (W ^ 3 x i u)) X2 + C ^ 2 (W ^ 4 x i u)) X3+ C ^ 2 (W ^ 5 x i u)) X4
Question 2.8:
h(x) = { 1 w ^ T * >= 2}
{0 0.w}
Question 2.9:
Take the negative log-likelihood
-log L(w) = ß / 2 Σ ^ N i = 1 || y (xn, w) – t n || N/2 log ß + N/ 2 log (2⊼) no dependence
Thus, miximing the log-likelihood equals miningizing
E(w) = ½ Σ n i = 1 || y(Xn, w) – tn || ^ 2
Question 3:
The reLu is a linear function that is used to give the output directly in positive way. If the output is not coming in positive then the output will come in the form of 0 (Wardah et al 2019). The de3fualt activation is there in this function and neural network with the different types of network. this model is also used in training performance.
Question 3.1:
ReLu is not linear.
Question 3.2:
It is a short or piecewise linear function that is used to give the output directly n a positive way (Raissi et al 2019). If the output is not coming in the positive then the output will come in the form of 0. This is the main reason it is considered a non-linear function that is used to perform in the neural network such as f(x) = max(0, X) In this equation X is the input value.
Question 4:
When we used to add both rows and columns ph of the padding and the total pw rows and columns so the output will be,
“(nh _) Kh + ph + 1) * (nw – kw + pw + 1) “
This equation tells that the output of the is used to increase by pw and ph respectively.
Now, there is a need to set a “ph = kh – 1 and pw = kw -1 it will help to give output and input which have the same width and height. This equation will help to predict the output of the following equation.
Lets us assume kh is add here, we used to pdd the following equation is ph/2 .
\
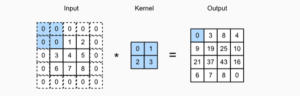
Figure 2: padding
(Source: self-created in Ms word)
Question 5:
It is a type of machine learning algorithm that is used to represent the ground between the unsupervised and supervised algorithms for machine learning (Saleem et al 2020). This algothroim has used the combination of two datasets that are unlabeled and labeled datasets at the time of the taring period (Vrejoiu, M.H., 2019. ). Semi-supervised learning is very important because it use to lies between unsupervised and supervised machine learning.
Question 6.1:
In deep learning, all the algorithms are used based on machine learning. This is the main reason that the problem that occurs due to machine learning is used to solve with the help of deep learning (Jospin et al 2022). The prediction is fully based on the algorithm of the Ml and the problem that is used to occur due can be solved by deep learning. The algorithm of deep learning is complex but it is always used to give the right answer.
Question 6.2:
Deep learning is basically machine learning and the AI that used to work as a human and provided a different type of result from it. It is a very important element of data science because it includes the predictive and statistical modeling of data science.
Reference list
Journals
Aggarwal, C.C., 2018. Neural networks and deep learning. Springer, 10, pp.978-3.
Jospin, L.V., Laga, H., Boussaid, F., Buntine, W. and Bennamoun, M., 2022. Hands-on Bayesian neural networks—A tutorial for deep learning users. IEEE Computational Intelligence Magazine, 17(2), pp.29-48.
Raissi, M., Perdikaris, P. and Karniadakis, G.E., 2019. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational physics, 378, pp.686-707.
Saleem, M.H., Potgieter, J. and Arif, K.M., 2020. Plant disease classification: A comparative evaluation of convolutional neural networks and deep learning optimizers. Plants, 9(10), p.1319.
Vrejoiu, M.H., 2019. Neural networks and deep learning in cyber security. Romanian Cyber Security Journal, 1(1), pp.69-86.
Wardah, W., Khan, M.G., Sharma, A. and Rashid, M.A., 2019. Protein secondary structure prediction using neural networks and deep learning: A review. Computational biology and chemistry, 81, pp.1-8.
Know more about UniqueSubmission’s other writing services:

