COMP7066 Neuronal Analysis Assignment Sample
Abstract
The rate of spike count depends on the trial as per spikes and the total duration of trial. There are different types of “degrees of complexity” and various types of field application are properly shown. Their rate of firing is also different from the rat’s brain. In the case of “biological spiking neurons” the current input for injection is illustrated. There are different types of navigation systems of monitoring that take place. The graphical representation is visible in the MATLAB for different types of analysis. The energy used by the brain is calculated by a scale and it is called spiking rate. In each and every neuron, energy is most essential so the calculation of energy is also very much essential. The classification of firing-rate of rats’ brains is also clearly discussed in this research. Mainly, the spikes rate and firing rate of a rat’s brain will be discussed clearly. There are different tropes of noise and distortions that take place in the system so the output results will not be accurate. So the distortions create a bad impact on the MATLAB output result
1.0 Introduction
1.1 Introduction
The simulation of the spiking neurons with respect to large networks on the cortical columns of scale or the whole area like the section cortex become more feasible for the advances in simulator software as well as computer technology. In the same simulation results to experimental findings of the spiking neurons, it is most essential to employ models of neurons that accurately take actual dynamic neurons in order to create realistic stimuli. Dynamical models which reproduce the responses for the individual neurons that injected currents down step to the work of seminal Huxley as well as Hodgkin. Mainly neuronal analysis is one type of data analysis that can copy the working principle of “the rat brain”. Neuronal analysis can show yearly problems and the successful use.
1.2 Background of Neuronal Analysis
This research is very based on neuronal analysis of the rat’s brain. There are different “machine learning classification” that also takes place in this research. Decision making process is different in the case of animals (Das, and Babadi, 2020). Their rate of firing is also different from the rat’s brain. There are different types of computations of the brain possible for the different spikes. This time period is a very much essential factor of the computations of individual spikes. There are different types of behavioral decisions identified by the neuroscientists.
1.3 Aims and Objectives
The main aim of the research is to show all the behavioral decision making processes of rat brain. The classification of firing-rate of rats’ brains is also clearly discussed in this research. Mainly, the spikes rate and firing rate of a rat’s brain will be discussed clearly.
- To measure the equation model of membrane for a rats brain
- To analysis “real firing-rates” using decoder
- To discuss spikes generated from a special neuron model
1.4 Research Rationale
The mat lab computation is very much essential for neuronal analysis of rats’ brains. The spikes rate analysis and the firing rate analysis is dependent on the record because of the stronger axon. There are different types of spike times also visible in the MATLAB simulation. In the case of visual stimuli at the same time, the variations “from trial to trial” will be high. In input values have to be genuine for the output result of MATLAB simulation. There are different types of decoder (Duncan, et al 2018). It is essential most of the decoded is needed for continuous types of input. The generation of spikes for the neuron has to predictable every time. “Rate is more resilient to trial to trial variability than single spikes, some of it seems noise”. The principle of encoding can clearly discuss the neuron ensembles. The rate of spike count depends on the trial as per spikes and the total duration of trial.
2.0 Methodology
There are different types of methods used to calculate the spikes rate and the firing rate of rat. The spikes rate will be different for the real neuron and the model of neuron. The firing rate will also change to real neurons to model neurons. There are different types of Neuron models available but the “Izhikevich model” and the “augmented MAT model” will be discussed in this portion of the research. There are different types of features available in these two models (Galindo, et al 2020). In the case of “biological spiking neurons” the current input for injection is illustrated.
Spiking neural networks that copy neural gatherings have been concentrated broadly inside the setting of dynamical frameworks, and displayed as a bunch of differential conditions that oversee the fleeting advancement of its state factors. For a solitary neuron, the state factors are typically its film potential and the conductances of particle directs that intervene changes in the layer potential by means of motion of particles across the phone layer. A huge assortment of writing, going from the traditional HodgkinHuxley model, FitzHughNagumo model, Izhikevich model to more straightforward integrate and fire models, treats the issue of single cell sensitivity at different degrees of detail and biophysical believability. Individual neuron models are then associated through neurotransmitters, bottom up, to shape large scale spiking neural organizations.
These signs are electrochemical in nature and, similar to transfer races, travel from the cell assortment of one neuron through its vehicle stem or axon to the following neuron. Each such terminating signal is known as a spike or activity potential. Spikes are produced in light of upgrades or immediately, and each spike typically endures 1 millisecond.
Spike developments are essentially a blend arrangement of spikes and quiet. A typical method for pondering pinnacle development is a computerized succession of data. 1 is the pinnacle and 0 is the pinnacle (Glenwinkel, et al 2021). For instance, the encoded spike train structure resembles this: 001111101101. The initial two zeros address the stand by time between the introduction of the boost and the primary spike. Spike trains can be set off by actual tangible upgrades like sight, contact, smell, and sound. Then again, it tends to be created by unique boosts like B. Mental upgrades by bringing out memory.
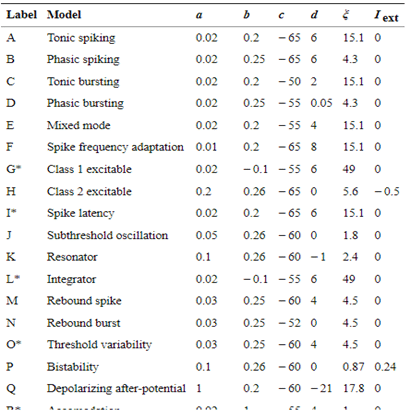
Figure 1: Parameters for Izhikevich model class obtained from code
(Source: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6208914/#Sec1title)
In these two models different types of parameters take place. Some of the parameters are identical and the other parameters not important for this study. The identical parameters are A, L, O, R and the L, R is not included in this research. In the case of the Izhikevich model G, L, R parameters have different types of equations (Hall, et al 2021). I and O parameters react as the A, M parameters of the Izhikevich neuron model. The parameter T is response as the time step in this neuron model.
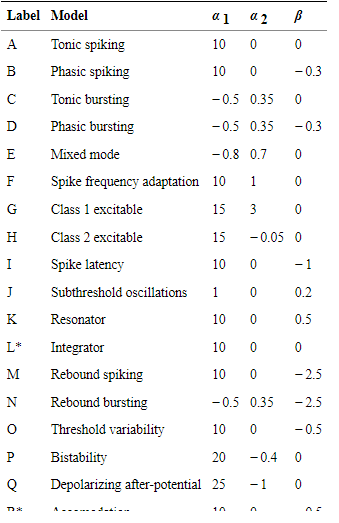
Figure 2: Different types of parameters for the AMAT neuron model class
(Source: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6208914/#Sec1title)
The AMAT neuron model also consists of twenty parameters. The parameters L and R are identical parameters and conjugate with the other parameters like A and O. In the case of AMAT model the potential equation for membrane will,
In the case of neuronal analysis, the response of a neuron is denoted by Istim(t) and it is used for different types of neuron scenarios. The full value of input neuron is receive as,
Here, Istim(t) = resulting value of current stimulus
Ibg(t) = input current for the noisy stationary background
In the AMAT model, the input current value of resulting noise can be calculated with mean and the standard deviation,
Here, τsyn,E = 1ms (constant of time)
τsyn,I = 3ms
wE, bg = 1PA (small weight for the injected current that is used in the background of the “Poisson Spike trains”.)
Energy use in cortex = spike rate of cortex* volume of cortex
Energy use in brain = Spike rate of brain* volume of brain
Energy use in cortex / Energy use in brain = (spike rate of cortex* volume of cortex)/(Spike rate of brain* volume of brain)
Firing rates of real and artificial neurons:
Firing rate of real neuron
In this human cerebrum, one normal neuron sends around 0.12 spikes each second.
While estimating cerebrum action, analysts might miss neurons that fire just sometimes during an examination (neurons with less action). By specially recording more dynamic neurons, the general terminating rate is misjudged. The predisposition is by all accounts as extensive as multiple times. This demonstrates that around 90% of neurons are quiet and hard to recognize in this kind of study. In this manner, many assessments should be diminished by a component of 10.
Informal Estimation:
“We don’t place much faith in unstructured webpages and publications that indicate neurons firing around 1 and 200 times per second 2 These sources lack references and are inconsistent, so we don’t trust them.”
Estimates of rate of firing in Neurons:
“According to the brain’s energy requirements, the average cortical neuron fires roughly 0.16 times every second.” The average cortical neuron does not appear to spike numerous times per second.
The central nervous system occupies a significant brain region. “It occupies around 80% of the brain’s volume3 but consumes 44 percent of its energy4.” It seems to include at least a quarter, if not that many, of both the brain’s synapses5. As a result, we might be able to utilize cortical neuronal firing frequencies as a good approximation for typical neuron firing speeds in the brain. One can also perform another more precise computation.
So, the calculation is shown below,
“energy (cortex) = volume(cortex) * spike_rate(cortex) * c”
“energy (brain) = volume(brain) * spike_rate(brain) * c”
“For c constant.”
Thus
“energy (cortex)/energy(brain)” = “volume(cortex)” * “spike_rate(cortex)/volume(brain)” * “spike rate(brain)”
“From the figures that are given above then, we can calculate:”
“0.44 = 0.8 * 0.16/spike_rate(brain)”
“spike_rate(brain) = 0.8 * 0.16 /0.44 = 0.29”
“Or for a high estimate:”
“0.44 = 0.8 * 1/spike_rate(brain)”
“spike_rate(brain) = 0.8 * 1 /0.44 = 1.82”
Thus, in view of this unpleasant extrapolation from the neocortical terminating rate, the normal cerebrum terminating rate is relied upon to be roughly 0.29 each second, maybe under 1.82 each second. Be that as it may, this is an exceptionally unpleasant computation and I’m not extremely certain with regards to the readings.
Estimate of firing of the neuron rate:
Investigations of the visual cortex of macaques and felines showed a normal of 34 spikes each second for felines and 1418 spikes each second for macaques under an assortment of conditions. Past investigations found nine pinnacles each second in felines 7. It is hard to tell how these assessments rely upon the imaged region and the creature analyzed, and it is considerably harder to make inferences from these outcomes. Likewise, these investigations seem, by all accounts, to be impacted by the above predisposition that main outwardly appealing cells are inspected. In this manner, they presumably misjudge all out neural action multiple times.
Highest rate of firing of the brain neurons:
“The ‘hard-headed period’ for a neuron is the time after it fires during which it either can’t fire once more (‘outright stubborn period’) or requires a particularly enormous boost to fire once more (‘relative headstrong period’).” As per physiologyweb.com, outright hard-headed periods will quite often be 12ms and relative stubborn periods will generally be 34ms.8 This suggests that neurons are for the most part not fit for terminating at in excess of 2501000 Hz (Ikhsan, et al 2019). This is interesting, but the site says nothing regarding the circulation of greatest terminating rates for various sorts of neurons, so the mean terminating rate could on a basic level be a lot higher.
3.0 Results and discussion
There are different types of artificial spike of model that take place in the neuron analysis. The membrane equations of the model are proposed in the research. With the specific datasheet the value is very much clear; the curve of the membrane equations model clearly shows the flow of voltage in time. In the case of reducing neuronal complexity a specific model is very much essential. The single type variable model can imply the valid limit of regime (Johnston, et al 2020). In the MAT Lab simulations of the research, the graphical representation is clearly visible that the value of voltage is minimized with respect to time. It is essential most of the decoded is needed for continuous types of input.
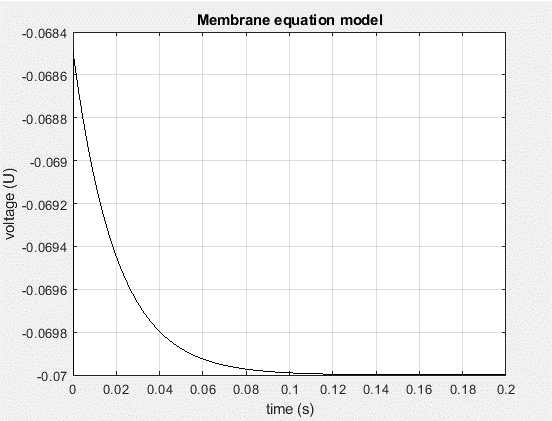
Figure 3: Output result of membrane equation model
(Source: Self-created in MATLAB)
In the above figure, graphical representation of the “membrane equation model” is clearly visible. Time vs. voltage graph is visible in this figure. It is clearly shown that the voltage decreases with respect to time(Kurkin, et al 2020). At the end of the time, the value of voltage becomes zero. The “LIF model” follows the primary functionality of living neurons, usually without considering the biological systems that make spiking to this above figure: “Axon-Hillock Neural Circuit”.
In this graph we have taken very short time frame as the time frame is very large, and also the data set is containing large amount of data. Spiking neural organizations (SNNs) are artificial neural organizations that better copy regular neural organizations. At the point when the layer potential arrives at the limit, the neuron flames and creates a sign that is sent to different neurons.
This sign increments or diminishes the potential as per the sign. A neuron model that fires when a limit is surpassed is otherwise called a spiking neuron model.Therefore, many recent discoveries have happened doing this figure for the ease of performing “LIF neural circuits”. Reports of “LIF circuits” that try to reintroduce extra-biological characteristics can be observed.
Those ideas all include systems that mimic different complex expressions than do typically located in “LIF neural models”, such as “bursting behavior” in which each neuron generates high-frequency discharges of heads in reply to huge values of excitation, including “SFA”, where the neuron adjusts to points of increased excitation by decreasing its head rotation (Sheikhattar, et al 2018).
The classification of firing-rate of rats’ brains is also clearly discussed in this research. Mainly, the spikes rate and firing rate of a rat’s brain will be discussed clearly.
These changes to the “LIF model” support the idea of “neuromorphic circuits” that hold the training capacity of extra network models while being small and comparatively uncomplicated to perform.
There are around 100 billion neurons in our mind, which continually convey messages to speak with one another. The background current fluctuates within the refractory period so the output result will fluctuate at the same time (Varderidou-Minasian, et al 2020).
The threshold voltage is taken -30mV and the period of refractory is taken 6ms. There are different tropes of noise and distortions that take place in the system so the output results will not be accurate. So the distortions create a bad impact on the MATLAB output result.
4.0 Conclusion
At the end of this project, it can be concluded that, this research is successfully completed. There are different types of functions are involved in the neuronal analysis. Different types of models and the analysis is alto takes place in this research. All the parameters of the research is successful discussed. In the case of reducing neuronal complexity a specific model is very much essential. This time period is a very much essential factor of the computations of individual spikes. The generation of spikes for the neuron has to predictable every time. There are two types of models of neuronal is discuses very much clearly. The AMAT neuron model also consists of twenty parameters. There are different types of navigation systems of monitoring that take place. There are different types of navigation systems of monitoring that take place. The software a portion of the research is also successfully completes. There graphical representation is also clearly visible.
Reference List
Journals
Das, P. and Babadi, B., 2020. Multitaper spectral analysis of neuronal spiking activity driven by latent stationary processes. Signal Processing, 170, p.107429.
Duncan, A., Klassen, E. and Srivastava, A., 2018. Statistical shape analysis of simplified neuronal trees. The Annals of Applied Statistics, 12(3), pp.1385-1421.
Galindo, S.E., Toharia, P., Robles, Ó.D., Ros, E., Pastor, L. and Garrido, J.A., 2020. Simulation, visualization and analysis tools for pattern recognition assessment with spiking neuronal networks. Neurocomputing, 400, pp.309-321.
Glenwinkel, L., Taylor, S.R., Langebeck-Jensen, K., Pereira, L., Reilly, M.B., Basavaraju, M., Rafi, I., Yemini, E., Pocock, R., Sestan, N. and Hammarlund, M., 2021. In silico analysis of the transcriptional regulatory logic of neuronal identity specification throughout the C. elegans nervous system. Elife, 10, p.e64906.
Hall, B.E., Macdonald, E., Cassidy, M., Yun, S., Sapio, M.R., Ray, P., Doty, M., Nara, P., Burton, M.D., Shiers, S. and Ray-Chaudhury, A., 2021. Transcriptomic analysis of human sensory neurons in painful diabetic neuropathy reveals inflammation and neuronal loss. bioRxiv.
Ikhsan, M., Palumbo, A., Rose, D., Zille, M. and Boltze, J., 2019. Neuronal stem cell and drug interactions: A systematic review and meta‐analysis: Concise review. Stem cells translational medicine, 8(11), pp.1202-1211.
Johnston, K.G., Grieco, S.F., Yu, Z., Jin, S., Shen, T., Crary, R., Guzowski, J., Holmes, T., Nie, Q.C. and Xu, X., 2020. Robust population single neuronal calcium signal extraction using SCOUT allows for longitudinal analysis of behavior-associated neural ensemble dynamics. bioRxiv.
Kurkin, S., Chholak, P., Pisarchik, A. and Hramov, A., 2020, September. Analysis of the features of brain neuronal sources during imagery motor activity: MEG study. In 2020 4th Scientific School on Dynamics of Complex Networks and their Application in Intellectual Robotics (DCNAIR) (pp. 154-157). IEEE.
Sheikhattar, A., Miran, S., Liu, J., Fritz, J.B., Shamma, S.A., Kanold, P.O. and Babadi, B., 2018. Extracting neuronal functional network dynamics via adaptive Granger causality analysis. Proceedings of the National Academy of Sciences, 115(17), pp.E3869-E3878.
Varderidou-Minasian, S., Hinz, L., Hagemans, D., Posthuma, D., Altelaar, M. and Heine, V.M., 2020. Quantitative proteomic analysis of Rett iPSC-derived neuronal progenitors. Molecular autism, 11, pp.1-15.
Wertenbroek, R., Thoma, Y., Mor, F.M., Grassi, S., Heuschkel, M.O., Roux, A. and Stoppini, L., 2021. SpikeOnChip: A Custom Embedded Platform for Neuronal Activity Recording and Analysis. IEEE Transactions on Biomedical Circuits and Systems, 15(4), pp.743-755.
Zafar, A. and Hong, K.S., 2018. Neuronal activation detection using vector phase analysis with dual threshold circles: A functional near-infrared spectroscopy study. International journal of neural systems, 28(10), p.1850031.
………………………………………………………………………………………………………………………..
Know more about UniqueSubmission’s other writing services:
Essay Writing Help
Dissertation Writing Help
Case Studies Writing Help
MYOB Perdisco Assignment Help
Presentation Assignment Help
Proofreading & Editing Help

