HA1011 Assignment 2020
- Frequency distribution using 10 classes, stating the Frequency, Relative Frequency, Cumulative Relative Frequency and Class Midpoint.
| Summary Statistics and Graphs | |
| Mean | 954.3667 |
| Standard Error | 90.65369 |
| Median | 715 |
| Mode | 401 |
| Standard Deviation | 702.2005 |
| Sample Variance | 493085.5 |
| Kurtosis | 1.604551 |
| Skewness | 1.406397 |
| Range | 2816 |
| Minimum | 169 |
| Maximum | 2985 |
| Sum | 57262 |
| Count | 60 |
| Bin | Frequency |
| 100-300 | 6 |
| 301-600 | 19 |
| 601-900 | 9 |
| 901-1200 | 11 |
| 1201-1500 | 4 |
| 1501-1800 | 5 |
| 1801-2100 | 1 |
| 2100-1800 | 1 |
| 2400-2700 | 1 |
| 2700-3000 | 3 |
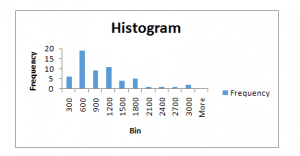
- Using (a), construct a histogram.
- Mean, median and mode
| Mean | 954.3667 |
| Median | 715 |
| Mode | 401 |
Question 2
- Is above a population or a sample? Explain the difference.
The above data presented in the context of the sample instead of population because information clearly shows that it is 7 weeks data. The term sample refers to a group of members of population selected for participants in the research study. Beside of this, population indicates to select all elements possessing with common features. It includes the each and every unit in the study (Ayyub & McCuen, 2016).
- Calculate the standard deviation of the weekly attendance. Show your workings.
| Weeks | Weekly attendance |
| 1 | 472 |
| 2 | 413 |
| 3 | 503 |
| 4 | 612 |
| 5 | 399 |
| 6 | 538 |
| 7 | 455 |
| Standard deviation | 74.06046436 |
- Calculate the Inter Quartile Range (IQR) of the chocolate bars sold
| Inter Quartile Range | |
| Quartile 1 | 434 |
| Quartile 2 | 472 |
| Inter Quartile Range | 38 |
- Calculate the correlation coefficient.
From the calculation, it is found that the value of correlation coefficient is 0.967992639. It means that is a strong positive relationship between the both variables (Silverman, 2018).
Question 3
| SUMMARY OUTPUT | ||||||||
| Regression Statistics | ||||||||
| Multiple R | 0.967993 | |||||||
| R Square | 0.93701 | |||||||
| Adjusted R Square | 0.924412 | |||||||
| Standard Error | 224.5952 | |||||||
| Observations | 7 | |||||||
| ANOVA | ||||||||
| df | SS | MS | F | Significance F | ||||
| Regression | 1 | 3751817 | 3751817 | 74.37736 | 0.000346 | |||
| Residual | 5 | 252215 | 50442.99 | |||||
| Total | 6 | 4004032 | ||||||
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | Lower 95.0% | Upper 95.0% | |
| Intercept | 1628.689 | 605.9 | 2.688049 | 0.0434 | 71.1734 | 3186.205 | 71.1734 | 3186.205 |
| X Variable 1 | 10.67723 | 1.238051 | 8.624231 | 0.000346 | 7.494724 | 13.85974 | 7.494724 | 13.85974 |
From the calculation, it is found that the value of the Coefficient of Determination is found 10.67723. It means that it is means that value is great and there is effective relationship between that data set (Mendenhall et al., 2016).
Question 4
From the data provided, it is found that there are 193 participants were selected total from the Holmes and external. In this, it is found that there is 47.66% (92/193 *100) probability that a randomly chosen player will be from Holmes OR receiving Grassroots training.
B
In the context of external recruitment, it is found that 66 participants are selected in this, it is found that 55 are interested in scientific training and 12 are in grassroots training. From the calculation, it can be calculated that there is 27.98% (54/193*100) probability that a randomly selected player will be External AND be in scientific training (Wieneke, 2015).
C
In the Holmes Hounds Big Bash League cricket team, 127 persons are selected from Holmes that are interest in scientific training and Grassroots training. The calculation depicts that there is 27.56% (35/127*100) probability that he is in scientific training.
D
From the case study and calculation, it can be said that in Holmes Hounds Big Bash League, the training is independent from recruitment. It is because there is not specific standard and regulation on the training needs. Figures are showing that selected participant can select the training selection according to its preference instead of the any assistance.
Question 5
A.
P(AIX)= p(A)*p(XIA)/ p(A)* p(XIA)+ p(BC)*p(YZIBC) (Source: Quirk, 2018).
= (0.55*0.2)/(0.55*0.2)+(0.45*0.8)
=0.11/(0.11+0.36)
= 0.11/0.47
= 0.2340
B.
P(X)= P(A)*P(X)+ P(B)*P(X)+ P(C)*P(X)+ P(C)*P(X)
= 0.55*0.2+0.3*0.35+0.1*0.6+0.1*0.9
=0.11+0.105+0.06+0.09
= 0.365
Question 6
A.
P(X≤2)=P(X=0)+P(X=1)+P(X=2)
= (0.1)0(0.90)8 + (0.1)1(0.90)7 + (0.1)2(0.90)6
= 0.430+ (0.1*0.478) + (0.01*0.531)
= 0.430+ 0.0478 + 0.00531
=0.4831
B.
In one minute, average 4 people enter the store then the average number of customers entering every 2 minutes will be:
2*4= 8 people in every two minutes
Need to calculate:
P(X=9 l l=8)=89*e-8 /9Ị
= (134217728 * 0.000335463)/ 362880
= 45025.082/362880
=0.1241
Question 7
A.
P(x=2)
=
=
=
=2.3376
From z table, it is identified that probability p(z=2.3376) for X=2 will be 0.9904. So, for over $2 million, it will be P(x>2) = (1-p(x=2))
= 1-0.9904
= 0.0096
P(1<X<1.1)
=<
= < <0
=p(-0.2597)
= 0.3974
Question 8
A.
For sufficiently large sample sizes (n≥30), it is considered that the distribution of the sample means is approximately normal. In this case, the sample size is 50 or more than 30 means the distribution of the sample means should be normal (Quinlan et al., 2019). But the distribution is not normal then a Z-distribution to test assistant’s research findings cannot be used.
B.
11 Investors agree for investment as their proportion will be 11/45= 0.2444
=0.2444-0.30/SQRT((0.30*0.70)/45)
= -0.0556/SQRT(0.21/45)
=-0.0556/SQRT(0.004667)
=-0.0556/0.068313
= -0.8139
From table, p value will be 0.2090.
References
Ayyub, B. M., & McCuen, R. H. (2016). Probability, statistics, and reliability for engineers and scientists. CRC press.
Mendenhall, W. M., Sincich, T. L., & Boudreau, N. S. (2016). Statistics for Engineering and the Sciences, Student Solutions Manual. Chapman and Hall/CRC.
Quinlan, C., Babin, B., Carr, J., & Griffin, M. (2019). Business research methods. South Western Cengage.
Quirk, T. J. (2018). Excel 2016 in Applied Statistics for High School Students. Springer.
Silverman, B. W. (2018). Density estimation for statistics and data analysis. Routledge.
Wieneke, B. (2015). PIV uncertainty quantification from correlation statistics. Measurement Science and Technology, 26(7), 074002.


