MN7022 FINANCIAL ANALYSIS AND INVESTMENT ASSIGNMENT SAMPLE
Module code and Title: MN7022 FINANCIAL ANALYSIS AND INVESTMENT ASSIGNMENT SAMPLE
Section A
I) Introduction
In business to attain success and make a crucial business decision, it is very important to understand the requirements of the company and its activities. Apart from that, it is also very essential to determine or analyze the financial reports of the company. Moreover, it is also identified that before making any investment-related decision it is very important to evaluate whether the decision of investment would be profitable for the company or not. Further, the paper involves essential illustrations in the context of the CAPM model and its impact on the procedure of making profitable financial or business decisions. Based on the provided description, therefore, it can be said that the main aim of the paper is to critically analyze the validity and criticism related to the CAPM model. Along with that in the further content, a necessary description in context to the alternative proposed model of CAPM model has also been provided.
II) Critical and analytical discussions
Critical discussion in context to the capital asset pricing model concerning its validity and criticism.
Definition
According to the ascertained knowledge it is perceived that the CAPM provides the necessary description regarding the procedure of financial market price securities. Moreover, it also explains the expected investment capital return. Apart from that, it is also notified that the model of capital asset pricing further provides a methodology for calibrating risk (Arribas et al. 2020, p. 2). On the other hand, it is also utilized while making any investment-related decision to translate the investment risk into the expected estimates of equity return. Therefore, based on the provided description it can be said that the CAPM is a model of finance that is mainly implemented in the business procedure or activities to evaluate the expected investment or assets rates of return. Moreover, it is also notified that CAPM is also referred to as the set of predictions that is incurred to balance the estimate of the return on assets that are risky (Wihartati and Efendi, 2021, p.19).
Based on further analysis and interpretation it is identified that the CAPM model is mainly utilized to determine or identify the expected return for a security. Apart from that, it is also notified that the CAPM further provides an advantage of comparing the addition of beta and risk-free returns. The observation and analysis further instruct that to properly or efficiently access the CAPM it is very important to acknowledge and recognize the unsystematic risk as well as the systematic risk of investment (Heikal, J., 2022, p. 21).
Hence, concerning the provided illustration it can be said that the implication of CAPM plays an essential role in the business and in the procedure of making a profitable investment decision. Further, the analysis also resembles that the CAPM is considered the widely used model of asset pricing in the theory of modern securities (Latunde et al. 2020, p. 20). The implication of CAPM further obliges the investors to make risk-free decisions regarding the investment. The model further helps the investors to look further for different measures through which the investment risks can be mitigated easily or minimized. Apart from that the utilization of CAPM further helps investors to maximize the expected return.
The estimation of CAPM is further based on the formula that has been provided below.
“E(ri) = Rf + βi(E(rm) – Rf)”
“E(ri) = financial asset required return i”
“Rf = risk-free return rate”
“Βi = beta value for the financial asset i”
“E(rm) = average return on the market of capital”
Assumptions of CAPM
Based on the given description and further observation it is notified that the model of asset pricing is often criticized. It is further advocated that the model is considered unrealistic due to the involvement of the assumptions while implementing it in the activities of investment on which it is actually based. Therefore, it can be said that before making any decision concerning the CAPM it is very important to be aware of the assumptions made by it and the actual reasons behind its criticism (Peng, S., 2021, p. 2239). The assumptions that CAPM involves are provided below:
The diversified portfolios are held by the investors: According to the stated assumption or prediction, it is articulated that the prediction further means that the investors would only require a systematic return of risk for their portfolios (Leković, 2018, p. 171). The assumption further indicates that the unsystematic risks are diversified and therefore those risks can be easily neglected.
Transaction horizon of a single period: According to further analysis it is determined that it is considered the second assumption of the CAPM. The description and observation further determine that CAPM assumes or predicts the standardized holding period of invested capital (Qoqiauri and Qoqiauri, 2019, p. 17 and 18). It is generally assumed or predicted to compare the return on different securities. It is further ascertained that the return over 6 months can not be compared with that of the 12 monthly returns. Therefore, it is ascertained that to ignore such issues the holding period of 1 year is mainly utilized.
Investors can easily lend or borrow capital at the risk-free return rate: As per the stated assumption, it is determined that this is the 3rd assumption of CAPM made by the theory of portfolio with the help of which CAPM was developed (Kruschwitz et al. 2019, p. 4). The stated assumption further gives a minimum level of return that is actually required by the potential investors. This can further be illustrated in the below provided SML graph.
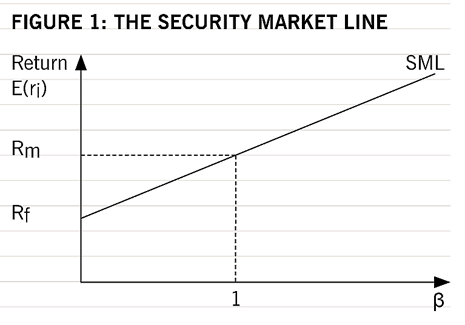 Figure 1: Graph determining the SML (Source: accaglobal.com, 2022)
Figure 1: Graph determining the SML (Source: accaglobal.com, 2022)
According to the provided graph, it is acknowledged that there exists a corresponding relationship between risk-free return rate and the security line of the market (accaglobal.com, 2022). The image further indicates that a risk-free rate of return correspondingly intersects the SML. SML is further also referred to as the graphical representation of the formula of CAPM.
The perfect market of capital: It is also identified or notified as one of the most essential assumptions of CAPM. According to the stated assumptions, it is determined that all securities of the market are correctly valued and the returns of every security are further plotted onto the market line of securities (Blitz, D., 2020, p. 3). The analysis further resembles that the stated assumptions further require that there should not be the involvement of transaction costs or taxes. The assumption further coveys that the investors must bear perfect knowledge in context to the valuation of securities and the risk associated with it so that they could easily have certain expectations that the investors are averse to risk and the market involves a large number of buyers and sellers.
Validity
According to further analysis, it is ascertained and acknowledged that the CAPM model is not considered valid anymore. The main reason that has been identified behind the counterfeit of CAPM is that the return calculated by this model does not interpret the reliable or actual position of the invested capital. Further, it is notified that the CAPM is considered a non-valid model because it is not always beneficial to rely upon the predictions of CAPM. More illustrations in context to the validity or non-validity of the CAPM model can be discussed concerning its advantages and disadvantages. The pros and cons of CAPM have been provided below in great detail.
Advantages
- The major advantage of the CAPM model is that it only emphasizes systematic risk (Giese et al. 2019, p. 2).
- Another benefit of CAPM is that it is derived theoretically and further also focuses on the relationship between systematic risk and required return (Xiao, Y., 2022, p. 2495).
- The involvement of the computation of equity cost is further considered as another advantage of the CAPM.
- It is further considered as the superior model as compared to that of WACC.
Disadvantages
- The most crucial disadvantage of CAPM is that it assigns values to the variables of CAPM (Ajrapetova, 2018, p. 42).
- It becomes sometimes quite challenging to implement or utilize the CAPM in the appraisal method of investment.
- The involvement of a single period time horizon is further considered as another disadvantage of the chosen model.
Explanation with reference to the alternative proposed models of CAPM
Based on further observation it is determined that the APT is considered the alternative to CAPM. It is further ascertained that APT emphasizes or implements fewer assumptions as compared to the CAPM. Therefore, based on the provided description it can be said that relying upon the APT model would be more beneficial for investors as compared to that of CAPM as it involves less assumption to evaluate the rate of risk-free return. It is also articulated as per the further interpretation that the APT model is developed concerning that the security prices are further driven by different factors that can either be considered as company-specific factors or macroeconomic factors.
APT is further also referred to as Arbitrage pricing theory and it is determined as the multi-factor model of asset pricing. The identified alternative model of CAPM is further determined that it is based upon the idea that the return on assets can be assumed utilising the linear relationship between the return expected on assets and the number of variables of macroeconomics that further captures systematic risk (Lento et al. 2019). Further, concerning the assumptions of APT, it is identified that it further involves three assumptions that are mentioned below.
- Absence of arbitrage opportunities in case of well-diversified investment portfolios.
- The investors have the authority of creating or building the assets portfolio by estimating the specified risk through diversification (Suroso et al. 2018, p. 1097)
- The return on assets can further be illustrated by different systematic factors.
The formula of APT is:
“Ri = αi + βi Rm + ei”
Where:
“Ri = return stock i”
“αi = alpha stock i”
“βi = beta stock i”
“Rm = market return”
“ei = random error”
The APT two-factor model formula is:
“Ri = αi + Βif1+Βif2 + …. + Βifn+ei”
Where:
“Ri = rate of return securities i”
“αi = rate of return for securities i if the systematic risk is zero”
“Β1, 2,..n = sensitivity of securities i to factors is considered”
“F1, 2,..n = surprise for a factor (actual value-expected value)”
“ei = term random error”
Further, it is determined that APT offers an opportunity for portfolio diversification for the investor and therefore, it is considered the most essential model of asset pricing. Moreover, it is also articulated that the chosen model further also involves the selection of risk and profiles of return that is further based on the premium and sensitivity to the different risk factors of the macroeconomy. Hence, it is also considered the general theory of asset pricing (Siregar, 2019, p.). It further helps to understand or recognize the price of assets in any international business marketplace. Apart from that, it is further notified that the implication of APT further makes it easier to illustrate the expected price of an asset (Siregar, 2019, p.745). The advantage of APT is that it concentrates more on the different factors of risk despite assets. The limitation of APT is that the theory does not provide any suggestions for the factors of particular assets and stocks.
III) Conclusion
Based on the provided description it is determined that before making any sort of investment-related decision it is very important to recognize the risk associated with different asset pricing models. From the provided description it is further considered that the CAPM and APT model plays an essential and significant role in the procedure of estimating risk-free returns on investment and assets. Moreover, it is also certified that the CAPM involves certain assumptions concerning which it is further considered as a non-valid asset pricing model. Based on the given descriptions it is further articulated that as compared to that CAPM, the APT model of evaluating assets’ price and risk-free return is more reliable. Further, it is ascertained that the APT model also involves certain assumptions based on which it is ordained that opting for APT would be more beneficial for the investors as compared to that CAPM. Moreover, concerning the advantages and disadvantages of both models, it is articulated or concluded that APT is more valid than CAPM.
Section B
Executive Summary
“Capital asset pricing model (CAPM)” is one of the key roles when a person looks forward to investing in the stock as this helps the investor to invest in the market by reducing the risk and maximizing the profit to the maximizing. It helps to show the equity that has a good return and it does not take into consideration that the dividend that has been given by the company has been ignored under the CAPM method. Thus to calculate the CAPM a systematic procedure is to be followed in order to get the right result. So for this project, seven stocks have been selected in order to bring out the weightage in which the investor can put his money by taking into consideration the value of the volatility that the stocks possess. The stocks that have been taken into consideration are “First republic bank, Akamai technology, carnival corporation plc, Wynn resort, Verisign, Haliburton, and BorgWarner”. These stocks are being traded in the NYSE market and in context to this stock the index that is being considered is S&P 500 index. This index includes the top 500 companies in terms of market capitalization that are listed on the NYSE.
Each stock’s monthly rate of return
To calculate CAPM the first thing that is needed is the data. The stock value of every month has been taken from all the seven Stocks and also the S&P 500 of the last 10 years. This data can be used for comparing the stocks on the monthly basis. As suggested by Martin et al. (2021, p.10) the change in the percentage of the stock value compared to last month can be termed as the monthly return by the stock.
So for all the stocks, the monthly value of each stock has been computed before the calculation of the CAPM and it will also help the investors to analyze and compare the stock.
Estimating the CAPM value
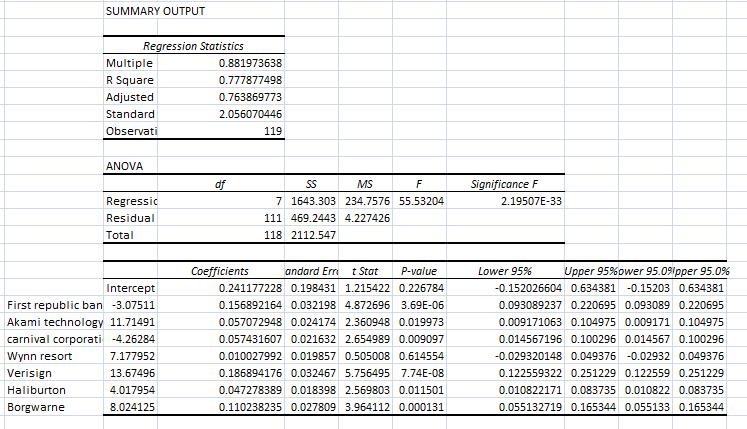 Figure 1: Regression by using the CAPM model (Source: Self-developed)
Figure 1: Regression by using the CAPM model (Source: Self-developed)
So for the calculation of the CAPM model, the regression model is used to calculate. So from the above table, it can be seen that the coefficient of the different stocks are “The CAPM model with the help of Regression Model is Y = 0.15*First republic bank + 0.06*Akamai technology 0.06*carnival corporation and plc + 0.01*Wynn resort + 0.19*Verisign + 0.04*Haliburton + 0.11*Borgwarne”. So as can be seen that the coefficient of all the stocks is less than 1. So, it can be concluded that the beta of all the stocks is less than one, this shows that the stocks are of low risk if they are invested for a longer period of time. So investors that are looking for a low-risk company for a long period of time then the investors can invest in these stocks.
Each stock’s standard deviation and stock variance
The two divergent mathematical concepts are “Variance and standard deviation (SD)”. This concept helps the investors to know the volatility of the stock and also this helps the investors and the institutes to make an investment. Volatility in the stock market is one of the most important features of stocks, A stock with high volatility is considered risky as it can move up or even down by a great percentage, whereas the low volatility stock move slowly and when there is a fall in the market they fall in less percentage in comparison to the high volatility fo the market.
As suggested by Rasekhschaffe and Jones, (2019, p.5) the possession of the price of the stock can be determined through the variance and SD. As we can see that these stocks are in the S&P 500 so it can be seen that the risk is low the monthly variance is “50.24, 73.87, 155.13, 173.87, 48.31, 198.97, and 83.61” and SD is “7.09, 8.59, 12.46, 13.19, 6.95, 14.11, and 9.14” for the companies “First republic bank, Akamai technology, carnival corporation and plc, Wynn resort, Verisign, Haliburton Borgwarner”.The investor who is more inclined to the risks towards the reward ratio should invest in the stocks (Spulbar et al. 2019, p.11). It has shown a great variance value for the SD that shows not near zero.
Increasing the rate of return with solver
| Companies | Optimal Weighted Portfolio |
| First republic bank | 0% |
| Akami technology | 0% |
| carnival corporation and plc | 0% |
| Wynn resort | 0% |
| Verisign | 100% |
| Haliburton | 0% |
| Borgwarne | 0% |
| Sum | 100% |
| Expected return | 67.707 |
| Risk | 24.108 |
| Sharpe Ratio | 2.691 |
Figure 2: Increasing returns utilizing Solver (Source: self-developed)
As per the basis of the above image, it has been done with assistance related to the solver. It provides increasing the expected return for the stocks by investing in the divergent seven stocks related to weightage which have been thought about. It is more important for investors at the time of making a higher profit (Pástor et al. 2022, p.22). It is required to make investments in the stock for earning and also increasing the profit for achieving the investor’s goal. Thus, with the effect of that, the model can recognize and be concerned about the higher profit. It can enjoy investing in divergent stocks in divergent ratios.
As per the above table, it can be seen that the stock’s weightage is mentioned at the value of “0.2, 0.2, 0.1, 0.1, 0.1, 0.1, and 0.2”. It is done with a respected organization then it receives the expected higher return. Thus, with the effect of that investors can be expected to invest at the value of @25.34%.
Thus, when the solver is utilized to increase the profit then it is seen by the investors. It should be invented on its money for VeriSign (Basher et al. 2018, p.15). It has achieved 67.707% at Maximum return. It would assist investors in fulfilling the maximizing profit objective. The risks have been denied in total.
Reducing the Sharpe ratio with solver
It is one of the major Sharpe ratios utilized with the differentiation for returning on making investing. It can be thought about the risks involved with the Sharpe ratio numerator is the comparison between the “expected or realized return and a benchmark” such as a “risk-free rate of return” (Curran and Zalla, 2020, p.14). Moreover, it is a performance-related investment category made in particular. It is one of the major disadvantages related to the Sharpe ratio, which denies the stock’s movement direction. The formula of Sharpe ratio calculation is mentioned at the value of “E[Ra-Rb]/σr]”.
Were,
“Ra = asset return, Rb = the risk-free rate, and σr = Sd of risk”.
The ratio of good shape is between 1 to 2, a better Sharpe ratio is between 2 to 3 for the best Sharpe ratio. Thus, the effect of that greater Sharpe ratio has shown better stock in the way of both “profit and risk” (Kliem and Ludin, 2019, p.6).
| Companies | Optimal Weighted Portfolio |
| First republic bank | 16% |
| Akami technology | 35% |
| carnival corporation and plc | 29% |
| Wynn resort | 6% |
| Verisign | 15% |
| Haliburton | 0% |
| Borgwarne | 0% |
| Sum | 100% |
| Expected return | 35.919 |
| Risk | 22.174 |
| Sharpe Ratio | 1.493 |
Figure 3: Increasing the Sharpe ratio by utilizing a solver (Source: Self-developed)
The stock’s weightage obtained for the random on the basis of the Sharpe ratio was calculated 1.07 times. Therefore, it happens at the time of solver taken for using the higher Sharpe ratio from 1.07 times to 1.516 times than weightage. It was determined with stock’s value by “35% in Akamai technology, 29% in carnival corporation and plc, 16% in First republic bank, 15% in Verisign, 6% in Wynn resort”. Along with that it has been made in Haliburton and Borgwarne by creating with investing can generally diminish the risks by enhancing the risk-return.
Reducing the risk with Solver
It reduces the portfolio risks which is important for increasing the profit. It has shown external factors for product stock as fall, its key investing aspect (Zhu et al. 2019, p.19). The accurate and proper knowledge related to risk participated in creating a portfolio assisting investors in saving capital. Along with that, it shows less exposure to the risk involved, assists one to be concerned for market volatility, and assists them in diminishing its risks.
| Companies | Optimal Weighted Portfolio |
| First republic bank | 13% |
| Akami technology | 53% |
| carnival corporation and plc | 13% |
| Wynn resort | 0% |
| Verisign | 0% |
| Haliburton | 12% |
| Borgwarne | 8% |
| Sum | 1 |
| Expected return | 22.727 |
| Risk | 22.941 |
| Sharpe Ratio | 0.868 |
Figure 3: Reduce the risk by utilizing a solver (Source: Self-developed)
The solver is being used to manage risk and reduce risk to a minimum, as shown by the weights of various stocks. Therefore, investors should invest the percentage shown in the above figure to reduce portfolio risk. The risk would fall to 22.94 percent as a result of this. Hence, From table 1, it very well may be likewise gathered that the one stock that is Akamai technology has enormous dangers implied as they are excessively unpredictable whereas the risk of all the other stocks is low (Van Gils et al. 2019, p.9). While Microsoft is the stock that is exceptionally safer contrasted with every one of the stocks. Therefore, an investor hoping to minimize risk should avoid investing in Akamai technology because these stocks involve significant risks (Velencoso et al. 2018, p.12).
| “Securities” | “Percentage of investment” |
| First republic bank | 13 |
| Akamai technology | 53 |
| carnival corporation and pl | 13 |
| Wynn resort | 0 |
| Verisign | 0 |
| Haliburton | 12 |
| Borg Warner | 8 |
Table 1: Investment Percentage (Source: self-developed)
Conclusion
As per the basis of the above analysis, it can be concluded that the CAPM model aids investors in making prudent stock investments. Therefore, using the Sharpe ratio in the CAPM model, they are able to construct a portfolio with the highest possible return and the lowest possible risk. It makes a difference and SD is a critical viewpoint to knowing the unpredictability of the stocks and assisting with understanding the gamble engaged with the stocks.
Therefore, an investor who is prepared to take a risk in exchange for a maximum return should invest in stocks such as Verisign. On the other hand, an investor who is looking for a maximum return with low risk should invest in Akamai technology as it also poses a low risk. In general, CAPM is a potent instrument for building an investor’s “investment portfolio” in accordance with their goals and objectives.
Reference list
accaglobal.com, 2022 CAPM: theory, advantages, and disadvantages Available at: https://www.accaglobal.com/gb/en/student/exam-support-resources/fundamentals-exams-study-resources/f9/technical-articles/CAPM-theory.html (Accessed on: 3rd December 2022)
Ajrapetova, T., 2018. Cross-Section of asset returns: Emerging markets and market integration. European Financial and Accounting Journal, 13(1), pp.41-60.
Arribas, I.P., Salvi, C. and Szpruch, L., 2020, October. Sig-SDEs model for quantitative finance. In Proceedings of the First ACM International Conference on AI in Finance (pp. 1-8).
Basher, S.A., Haug, A.A. and Sadorsky, P., 2018. The impact of oil-market shocks on stock returns in major oil-exporting countries. Journal of International Money and Finance, 86, pp.264-280.
Blitz, D., 2020. The risk-free asset implied by the market: Medium-term bonds instead of short-term bills. The Journal of Portfolio Management, 46(8), pp.120-132.
Curran, M. and Zalla, R., 2020. Can Volatility Solve the Naive Portfolio Puzzle?. arXiv preprint arXiv:2005.03204.
Giese, G., Lee, L.E., Melas, D., Nagy, Z. and Nishikawa, L., 2019. Foundations of ESG investing: How ESG affects equity valuation, risk, and performance. The Journal of Portfolio Management, 45(5), pp.69-83.
Heikal, J., 2022. Investment Decision Using Capital Asset Pricing Model (CAPM) in Indonesia’s Banking Sector. Journal of Economics, Finance and Accounting Studies, 4(4), pp.19-27.
Kliem, R.L. and Ludin, I.S., 2019. Reducing project risk. Routledge.
Kruschwitz, L., Löffler, A. and Lorenz, D., 2019. Divergent interest rates in the theory of financial markets. The Quarterly Review of Economics and Finance, 71, pp.48-55.
Latunde, T., Akinola, L.S. and Dare, D.D., 2020. Analysis of capital asset pricing model on Deutsche bank energy commodity. Green Financ, 2(1), pp.20-34.
Leković, M., 2018. Investment diversification as a strategy for reducing investment risk. Ekonomski horizonti, 20(2), pp.173-187.
Lento, G.L.D., Latif, I.N. and Verahastuti, C., 2019. Analisis Portofolio Saham Pada Perusahaan Sub Sektor Pertambangan Yang Terdaftar Di Bursa Efek Indonesia (BEI) Dengan Pendekatan Capital Asset Pricing Model (CAPM) dan Arbitrage Pricing Theory (APT). Journal of Indonesian Science Economic Research, 1(2), pp.12-19.
Martin, I.W. and Wagner, C., 2019. What is the Expected Return on a Stock?. The Journal of Finance, 74(4), pp.1887-1929.
Mazur, M., Dang, M. and Vega, M., 2021. COVID-19 and the march 2020 stock market crash. Evidence from S&P1500. Finance research letters, 38, p.101690.
Pástor, Ľ., Stambaugh, R.F. and Taylor, L.A., 2022. Dissecting green returns. Journal of Financial Economics, 146(2), pp.403-424.
Peng, S., 2021, December. The Validity of CAPM: A Critical and Conclusive Study with Empirical Evidence from the UK Security Market. In 2021 3rd International Conference on Economic Management and Cultural Industry (ICEMCI 2021) (pp. 2237-2243). Atlantis Press.
Qoqiauri, L. and Qoqiauri, N., 2019. Main Regulations of CAPM Model and Its Modern Modification. Management, 7(1), pp.15-32.
Rasekhschaffe, K.C. and Jones, R.C., 2019. Machine learning for stock selection. Financial Analysts Journal, 75(3), pp.70-88.
Siregar, E.I., 2019. The Impact of Political Risk and Macro Economics on Stock Return at Indonesia Stock Exchange (An Approach of Arbritage Pricing Theory (APT)). KnE Social Sciences, pp.744-772.
Spulbar, C., Ejaz, A., Birau, R. and Trivedi, J., 2019. Sustainable investing based on momentum strategies in emerging stock markets: A case study for Bombay Stock Exchange (BSE) of India. Scientific Annals of Economics and Business, 66(3), pp.351-361.
Suroso, S., Rusiadi, R.B., Purba, A.P.U., Siahaan, A.K., Sari, A.N. and Lubis, A.I.F., 2018. Autoregression Vector Prediction on Banking Stock Return using CAPM Model Approach and Multi-Factor APT. Int. J. Civ. Eng. Technol, 9(9), pp.1093-1103.
Van Gils, T., Caris, A., Ramaekers, K. and Braekers, K., 2019. Formulating and solving the integrated batching, routing, and picker scheduling problem in a real-life spare parts warehouse. European Journal of Operational Research, 277(3), pp.814-830.
Velencoso, M.M., Battig, A., Markwart, J.C., Schartel, B. and Wurm, F.R., 2018. Molecular firefighting—how modern phosphorus chemistry can help solve the challenge of flame retardancy. Angewandte Chemie International Edition, 57(33), pp.10450-10467.
Wihartati, A.P. and Efendi, T.F., 2021. Decision Support System for Share Investment Using The Capital Assetpricing Method (CAPM). International Journal of Computer and Information System (IJCIS), 2(1), pp.19-23.
Xiao, Y., 2022, March. Comparison of the Applicability of CAPM and Fama-French Model in Different Regions. In 2022 7th International Conference on Financial Innovation and Economic Development (ICFIED 2022) (pp. 2493-2496). Atlantis Press.
Zhu, M., Zheng, X., Wang, Y., Li, Y. and Liang, Q., 2019. Adaptive portfolio by solving multi-armed bandit via thompson sampling. arXiv preprint arXiv:1911.05309.
Know more about UniqueSubmission’s other writing services:

