Statistics and Forecasting Assignment Sample
Introduction
Economic statistics encompass any mathematical information which summarises previous activity or projects upcoming behaviour of a single capital product, a series of instruments, or marketplaces in a large geographical area. It is helpful to divide such statistics into 3 groups initially. Forecasting is a strategy which utilises previous information as insight to create accurate predictions about the route of upcoming developments. Forecasting is used by organisations to effectively manage their resources or prepare for unexpected costs in the future. Statistics and forecasting is a combination that is utilised by several sectors like stock markets, GDP analysis, product purchases and many more for the development. In this project the developer will try to analyse the concept and prepare a high accuracy model with the help of SPSS software.
Methodology
This research applied primary analysis to achieve their project aim and the complete dataset which is collected is passed through the pre data processing for an accurate result. Developers conducted two analysis processes, one is for the first case study where university teacher’s salary related problems are covered and in the second case study company’s size and their cooperation related effectiveness is mentioned.
Topic 1
First case study is about the US universities faculty members’ salary, where 787 participants contributed their point of view and those responses are considered as a dataset. The empirical study was conducted for some issues like the interviewer wanted to know about the faculty members phD years, salary, gender and also their designation, etc.
Determining Causal Factors
Here Dependent variable is Salary
Here chosen Independent Variable is Female/Male, Position, University, State, and Publication
In the collected dataset few minor errors are present but those errors are identified and rectified while the dataset is passing through the pre-processing phase. Developers determine the required causal factors with the help of correlation analysis and means analysis. In causal factor analysis developers determine the mean, median, standard deviation, error difference and the correlation between independent and dependent variables. This total analysis part is performed in the SPSS software (Á. and Zilberman, 2021.). To analyse the first case study the developers operate two regression methods one is Durbin-Watson test and the other one is VIF. These two analyses help the developers to gain the impact of the gender, position, university, etc. on their salary structure. Several issues are present in the university related to the teacher’s salary and this project conducted by the developers to establish a model which helps the university to identify what type of issues are available and how much the independent variables affect the dependent variable.
Dataset for Case Study 1:
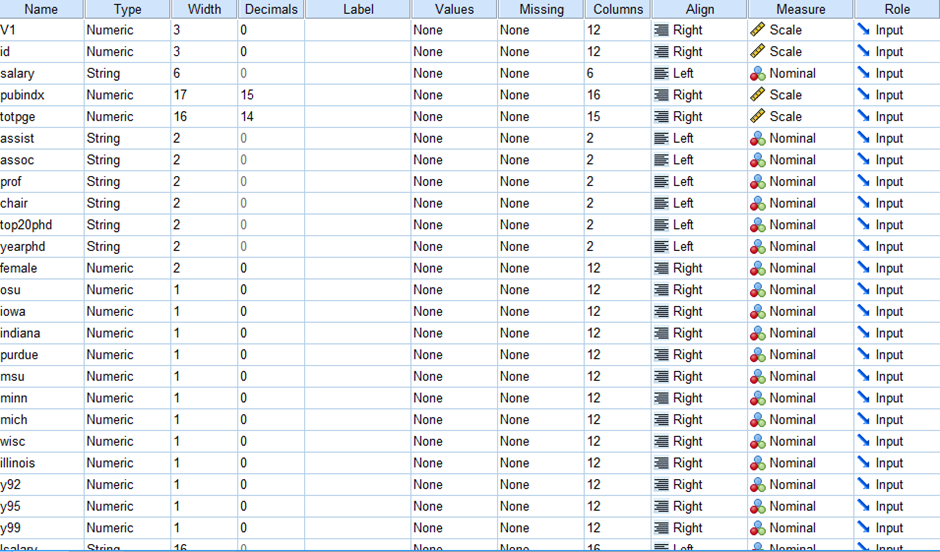
Figure 1: Dataset
Topic 2
Second case study about the UK based company’s innovation activities and their effectiveness or impact. Developers in this project try to establish a relationship or determine the impact of the independent and dependent variables on the UK based companies.
Determining Causal Factors
The Dependent variable is Innovation
The Independent Variable is Size and Cooperation
In this second case study the developers collected the dataset via primary research method and for that they passed the data through a pre-processing step where some errors are recognised and eliminated from the dataset (Vasconcelos, et al. 2021.). Developers again determine the causal factors for the second case study where they analyse correlation analysis and means analysis. Here the developers determine the mean, median, standard deviation, error difference and the correlation between independent and dependent variables. In this particular case study helps the developers to understand the impact of any company’s size as well as their cooperation activities on their innovation system. For appropriate results the developers perform ANOVA as well as cluster analysis.
Dataset for Case Study 2
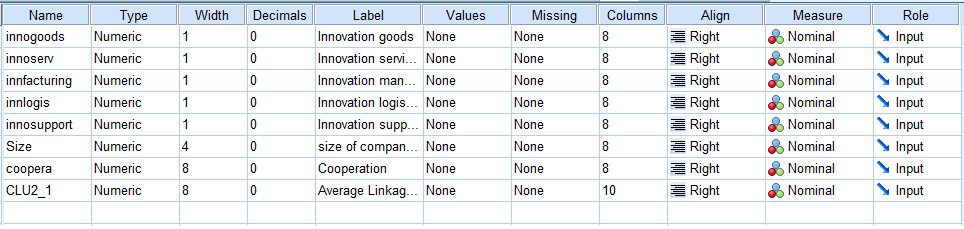
Figure 2: Dataset
Analysis and Result
Topic 1
Causal Factors
Means
Means analysis is performed by the developers where they consider salary as a dependent variable and female, position, university and state as an independent variable (Medeiros, et al. 2021. ). After means analysis developers get mean, median, standard deviation, error difference, maximum, minimum and range. The developers determine each and every independent variable’s mean, median, standard deviation, range, etc with respect to dependent variables. The result shows in the tables below which is the processing of the given case study.
| Cases | ||||||
| Included | Excluded | Total | ||||
| N | Percent | N | Percent | N | Percent | |
| salary * prof | 679 | 86.4% | 107 | 13.6% | 786 | 100.0% |
| salary * pubindx | 679 | 86.4% | 107 | 13.6% | 786 | 100.0% |
| salary * female | 664 | 84.5% | 122 | 15.5% | 786 | 100.0% |
| salary * osu | 679 | 86.4% | 107 | 13.6% | 786 | 100.0% |
| salary * indiana | 679 | 86.4% | 107 | 13.6% | 786 | 100.0% |
| salary * prof | |||||||
| salary | |||||||
| prof | Mean | Std. Deviation | Std. Error of Mean | Minimum | Maximum | Range | Median |
| 0 | 60574.77 | 14725.871 | 1122.837 | 18670 | 118962 | 100292 | 57721.00 |
| 1 | 93267.48 | 25672.520 | 1278.839 | 38200 | 191000 | 152800 | 89500.00 |
| NA | 74065.45 | 31046.216 | 3044.332 | 22254 | 223537 | 201283 | 66056.00 |
| Total | 82044.86 | 28168.631 | 1081.013 | 18670 | 223537 | 204867 | 78371.00 |
| salary * female | |||||||
| salary | |||||||
| female | Mean | Std. Deviation | Std. Error of Mean | Minimum | Maximum | Range | Median |
| 0 | 83776.46 | 28210.024 | 1145.954 | 18670 | 223537 | 204867 | 80043.00 |
| 1 | 68319.62 | 22946.900 | 3013.076 | 36050 | 139660 | 103610 | 61464.00 |
| Total | 82426.31 | 28116.404 | 1091.128 | 18670 | 223537 | 204867 | 78550.00 |
| salary * osu | |||||||
| salary | |||||||
| osu | Mean | Std. Deviation | Std. Error of Mean | Minimum | Maximum | Range | Median |
| 0 | 81798.40 | 28100.871 | 1151.057 | 18670 | 223537 | 204867 | 78290.00 |
| 1 | 83814.64 | 28761.133 | 3156.945 | 42648 | 181104 | 138456 | 78492.00 |
| Total | 82044.86 | 28168.631 | 1081.013 | 18670 | 223537 | 204867 | 78371.00 |
| salary * indiana | |||||||
| salary | |||||||
| indiana | Mean | Std. Deviation | Std. Error of Mean | Minimum | Maximum | Range | Median |
| 0 | 82254.70 | 28139.148 | 1126.467 | 18670 | 223537 | 204867 | 78550.00 |
| 1 | 79664.15 | 28653.749 | 3863.671 | 36050 | 191000 | 154950 | 74107.00 |
| Total | 82044.86 | 28168.631 | 1081.013 | 18670 | 223537 | 204867 | 78371.00 |
Correlation
Correlation assessment is generally a statistical tool applied in exploration to determine the intensity of a logistic connection across two factors as well as calculate their associations. Specifically stated, correlation investigation or examination computes the quantity of changes in one variable like a result of a variation into some other variables (P. and Loeffler, 2019. ). The correlation analysis helps the developers to identify the impact of gender, position, university on the other salary. In this analysis the correlation is signified at the level of 0.01. The below table shows the result of the analysis.
| Descriptive Statistics | |||
| Mean | Std. Deviation | N | |
| salary | 82044.86 | 28168.631 | 679 |
| female | .08 | .277 | 753 |
| osu | .12 | .323 | 786 |
| pubindx | 35.352493657467480 | 38.916367705071930 | 786 |
| indiana | .08 | .272 | 786 |
| Correlations | ||||||
| salary | female | osu | pubindx | indiana | ||
| salary | Pearson Correlation | 1 | -.155** | .023 | .494** | -.025 |
| Sig. (2-tailed) | .000 | .542 | .000 | .514 | ||
| Sum of Squares and Cross-products | 537973872496.262 | -818187.994 | 146891.368 | 368919446.445 | -130939.467 | |
| Covariance | 793471788.343 | -1234.069 | 216.654 | 544128.977 | -193.126 | |
| N | 679 | 664 | 679 | 679 | 679 | |
| female | Pearson Correlation | -.155** | 1 | .062 | -.201** | .117** |
| Sig. (2-tailed) | .000 | .092 | .000 | .001 | ||
| Sum of Squares and Cross-products | -818187.994 | 57.729 | 4.219 | -1638.304 | 6.729 | |
| Covariance | -1234.069 | .077 | .006 | -2.179 | .009 | |
| N | 664 | 753 | 753 | 753 | 753 | |
| osu | Pearson Correlation | .023 | .062 | 1 | .059 | -.108** |
| Sig. (2-tailed) | .542 | .092 | .100 | .002 | ||
| Sum of Squares and Cross-products | 146891.368 | 4.219 | 81.996 | 579.188 | -7.454 | |
| Covariance | 216.654 | .006 | .104 | .738 | -.009 | |
| N | 679 | 753 | 786 | 786 | 786 | |
| pubindx | Pearson Correlation | .494** | -.201** | .059 | 1 | -.138** |
| Sig. (2-tailed) | .000 | .000 | .100 | .000 | ||
| Sum of Squares and Cross-products | 368919446.445 | -1638.304 | 579.188 | 1188869.685 | -1147.327 | |
| Covariance | 544128.977 | -2.179 | .738 | 1514.484 | -1.462 | |
| N | 679 | 753 | 786 | 786 | 786 | |
| indiana | Pearson Correlation | -.025 | .117** | -.108** | -.138** | 1 |
| Sig. (2-tailed) | .514 | .001 | .002 | .000 | ||
| Sum of Squares and Cross-products | -130939.467 | 6.729 | -7.454 | -1147.327 | 57.950 | |
| Covariance | -193.126 | .009 | -.009 | -1.462 | .074 | |
| N | 679 | 753 | 786 | 786 | 786 | |
| **. Correlation is significant at the 0.01 level (2-tailed). | ||||||
Regression Analysis
Considering correlation, is the subsequent stage of the linear regression. While researchers wish to forecast the number of one variable depending on the position of the other variables, researchers utilise it. The factor they wish to forecast is referred to as the dependent parameter (or in sometimes, the output variable). In this project developers are use two methods to determine the respected values or to perform the regression analysis. Those are Durbin Watson test and the other one is VIF test. In the below section the analysis is present.
Durbin-Watson test
The ‘Durbin-Watson test’ gives an idea about the autocorrelation concept while a fixed value of ‘Durbin-Watson test’ defines the positive and negative as well as only autocorrelation. The mathematical value of zero to four is the limit of the ‘Durbin-Watson test’ result. Here if the value lies in between zero to less than two then positive autocorrelation occurs (Flaxman, et al. 2019. ). If the number lies in between 2 to 4 then that indicates the negative autocorrelation and if the value is two then that defines in the dataset no autocorrelation is present. In the below table the result is shown, where the ‘Durbin-Watson test’ value is 1.321. This value indicates positive correlation is present in this project.
| Model Summaryb | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate | Durbin-Watson | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | .547a | .299 | .294 | 22973.895 | 1.321 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. Predictors: (Constant), indiana, prof, osu, female | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. Dependent Variable: salary
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ANOVAa | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 127775945016.405 | 4 | 31943986254.101 | 60.523 | .000b |
| Residual | 299262506878.666 | 567 | 527799835.765 | |||
| Total | 427038451895.071 | 571 | ||||
| a. Dependent Variable: salary | ||||||
| b. Predictors: (Constant), indiana, prof, osu, female | ||||||
Charts
Figure 3: The Histogram representation of Durbin Watson test analysis
VIF
The “variance inflation factor (VIF)” justifies the degree of the multicollinearity in a collection of multivariate regression factors. This VIF used for a regression modelling factor is equivalent to the percentage of the total design variation to the volatility of the system with only that specific independent component. For every independent parameter, this proportion is computed (S. and Ratanavaraha, 2020.). A strong VIF suggests that the independent factor linked with this is significantly collinear among other components in the models. The VIF analysis helps the developers to understand if the system is correlated or not. The result of this analysis is 1.075 for female, 1.065 for positions, 1.015 for state and 1.022 for the university. The value indicates that this system is correlated.
| “Variables Entered/Removeda” | |||
| Model | Variables Entered | Variables Removed | Method |
| 1 | indiana, prof, osu, femaleb | . | Enter |
| a. Dependent Variable: salary | |||
| b. All the variables which are requested are entered. | |||
|
Coefficientsa |
|||
| Model | Collinearity Statistics | ||
| Tolerance | VIF | ||
| 1 | female | .930 | 1.075 |
| prof | .939 | 1.065 | |
| osu | .985 | 1.015 | |
| indiana | .978 | 1.022 | |
| a. Dependent Variable: salary | |||
|
Chart |

Figure 4: The Histogram representation of VIF analysis
Topic 2
Causal Factors
Means
Means analysis mainly conducted by the developers when they wish to summarise as well as compare variations in descriptive analysis among one or even more components or categorical data, the Comparison Means technique comes in convenient. For the second case study the dependent variable is innovation where the size and the cooperation are independent variables (Jomnonkwao, et al. 2020.). Here the developers calculate the mean, median, standard deviation, error difference, maximum, minimum and range, etc., with respect to the company’s size and their innovation. In the below table the result is shown which is the processing summary of the given case study.
| Cases | ||||||
| Included | Excluded | Total | ||||
| N | Percent | N | Percent | N | Percent | |
| Innovation support * size of company (staff) | 4922 | 52.2% | 4505 | 47.8% | 9427 | 100.0% |
| Report | |||||||
| Innovation support | |||||||
| size of company (staff) | Mean | Std. Deviation | Minimum | Maximum | Std. Error of Mean | Range | Median |
| 1 | .03 | .177 | 0 | 1 | .022 | 1 | .00 |
| 2 | .03 | .162 | 0 | 1 | .026 | 1 | .00 |
| 3 | .07 | .255 | 0 | 1 | .038 | 1 | .00 |
| 4 | .02 | .132 | 0 | 1 | .018 | 1 | .00 |
| 5 | .04 | .207 | 0 | 1 | .025 | 1 | .00 |
| 6 | .08 | .275 | 0 | 1 | .035 | 1 | .00 |
| 7 | .05 | .223 | 0 | 1 | .025 | 1 | .00 |
| 8 | .05 | .226 | 0 | 1 | .023 | 1 | .00 |
| 9 | .04 | .187 | 0 | 1 | .025 | 1 | .00 |
| 10 | .13 | .332 | 0 | 1 | .033 | 1 | .00 |
| 11 | .12 | .329 | 0 | 1 | .038 | 1 | .00 |
| 12 | .14 | .348 | 0 | 1 | .039 | 1 | .00 |
| 13 | .07 | .254 | 0 | 1 | .030 | 1 | .00 |
| 14 | .06 | .231 | 0 | 1 | .027 | 1 | .00 |
| 15 | .11 | .313 | 0 | 1 | .036 | 1 | .00 |
| 26 | .13 | .337 | 0 | 1 | .049 | 1 | .00 |
| 27 | .13 | .336 | 0 | 1 | .045 | 1 | .00 |
| 28 | .17 | .383 | 0 | 1 | .057 | 1 | .00 |
| 29 | .13 | .335 | 0 | 1 | .053 | 1 | .00 |
| 30 | .16 | .365 | 0 | 1 | .048 | 1 | .00 |
| 31 | .14 | .347 | 0 | 1 | .057 | 1 | .00 |
| 39 | .09 | .288 | 0 | 1 | .049 | 1 | .00 |
| 40 | .20 | .405 | 0 | 1 | .064 | 1 | .00 |
| 150 | .29 | .488 | 0 | 1 | .184 | 1 | .00 |
| 151 | .11 | .333 | 0 | 1 | .111 | 1 | .00 |
| 374 | .00 | . | 0 | 0 | . | 0 | .00 |
| 418 | .00 | . | 0 | 0 | . | 0 | .00 |
| 419 | .60 | .548 | 0 | 1 | .245 | 1 | 1.00 |
| 421 | .00 | .000 | 0 | 0 | .000 | 0 | .00 |
| 984 | 1.00 | . | 1 | 1 | . | 0 | 1.00 |
| 993 | .00 | . | 0 | 0 | . | 0 | .00 |
| Total | .20 | .403 | 0 | 1 | .006 | 1 | .00 |
Correlation
For the second case study the developers develop the relationship between innovation factors and companies cooperation. Here each innovation factor like innovation goods, services, manufacturing, legislation and support are considered by the developers. For each innovation mean, median, standard deviation, error difference, maximum, minimum and range, etc are calculated. This analysis shows the effect of the cooperation on UK based companies’ innovation factors. In the below table the obtained result is shown.
| “Innovation goods Innovation services Innovation manufacturing Innovation logistics Innovation support * Cooperation” | ||||||
| Cooperation | Innovation goods | Innovation services | Innovation manufacturing | Innovation logistics | Innovation support | |
| 0 | Mean | .31 | .07 | .25 | .07 | .13 |
| Std. Deviation | .463 | .254 | .431 | .254 | .339 | |
| Minimum | 0 | 0 | 0 | 0 | 0 | |
| Maximum | 1 | 1 | 1 | 1 | 1 | |
| Std. Error of Mean | .008 | .004 | .007 | .004 | .006 | |
| Range | 1 | 1 | 1 | 1 | 1 | |
| Median | .00 | .00 | .00 | .00 | .00 | |
| 1 | Mean | .69 | .22 | .64 | .21 | .39 |
| Std. Deviation | .461 | .416 | .479 | .406 | .489 | |
| Minimum | 0 | 0 | 0 | 0 | 0 | |
| Maximum | 1 | 1 | 1 | 1 | 1 | |
| Std. Error of Mean | .013 | .011 | .013 | .011 | .013 | |
| Range | 1 | 1 | 1 | 1 | 1 | |
| Median | 1.00 | .00 | 1.00 | .00 | .00 | |
| Total | Mean | .42 | .11 | .35 | .11 | .20 |
| Std. Deviation | .493 | .314 | .478 | .309 | .403 | |
| Minimum | 0 | 0 | 0 | 0 | 0 | |
| Maximum | 1 | 1 | 1 | 1 | 1 | |
| Std. Error of Mean | .007 | .004 | .007 | .004 | .006 | |
| Range | 1 | 1 | 1 | 1 | 1 | |
| Median | .00 | .00 | .00 | .00 | .00 | |
ANOVA
ANOVA is an abbreviation for ‘assessment of variation,’ thus it applies to a quantitative method that separates reported variance data into several parts for use in subsequent studies. The ANOVA analysis has been utilised to understand the relationship between dependent parameters as well as independent factors for three or multiple pairs of measurements. ANOVA assesses whether or not variation among different groups of observations are statistically significant. This analysis helps to examine the levels of changes across the subcategories employing examples drawn from each person’s information. In this project the developers consider each variable of the innovation to establish the relationship between the independent variable and the dependent parameters. All the values of innovations are shown in the below table.
| ANOVA | ||||||||
| Sum of Squares | df | Mean Square | F | Sig. | ||||
| Innovation goods | Between Groups | (Combined) | 143.076 | 1 | 143.076 | 669.079 | .000 | |
| Linear Term | Unweighted | 143.076 | 1 | 143.076 | 669.079 | .000 | ||
| Weighted | 143.076 | 1 | 143.076 | 669.079 | .000 | |||
| Within Groups | 1052.095 | 4920 | .214 | |||||
| Total | 1195.171 | 4921 | ||||||
| Innovation services | Between Groups | (Combined) | 22.880 | 1 | 22.880 | 242.957 | .000 | |
| Linear Term | Unweighted | 22.880 | 1 | 22.880 | 242.957 | .000 | ||
| Weighted | 22.880 | 1 | 22.880 | 242.957 | .000 | |||
| Within Groups | 463.330 | 4920 | .094 | |||||
| Total | 486.210 | 4921 | ||||||
| Innovation manufacturing | Between Groups | (Combined) | 152.643 | 1 | 152.643 | 771.288 | .000 | |
| Linear Term | Unweighted | 152.643 | 1 | 152.643 | 771.288 | .000 | ||
| Weighted | 152.643 | 1 | 152.643 | 771.288 | .000 | |||
| Within Groups | 973.701 | 4920 | .198 | |||||
| Total | 1126.344 | 4921 | ||||||
| Innovation logistics | Between Groups | (Combined) | 18.634 | 1 | 18.634 | 202.859 | .000 | |
| Linear Term | Unweighted | 18.634 | 1 | 18.634 | 202.859 | .000 | ||
| Weighted | 18.634 | 1 | 18.634 | 202.859 | .000 | |||
| Within Groups | 451.940 | 4920 | .092 | |||||
| Total | 470.574 | 4921 | ||||||
| Innovation support | Between Groups | (Combined) | 66.683 | 1 | 66.683 | 448.969 | .000 | |
| Linear Term | Unweighted | 66.683 | 1 | 66.683 | 448.969 | .000 | ||
| Weighted | 66.683 | 1 | 66.683 | 448.969 | .000 | |||
| Within Groups | 730.741 | 4920 | .149 | |||||
| Total | 797.424 | 4921 | ||||||
Cluster
Cluster analysis seems to be the collection of techniques as well as methods employed in the statistics to categorise diverse things into clusters so that the resemblance among two items is greatest if they correspond to the identical category as well as minimal elsewhere. Cluster analysis is performed by the developers to determine the similarity which may be available in the collected dataset. Cluster analysis observes the complete dataset and after that the result helps the UK based companies to understand their customer’s behaviours and their connections with their products. In the below table the obtained result is present.
| Case Processing Summaryb,c | |||||||
| Cases | |||||||
| Valid | Rejected | Total | |||||
| Missing Value | Out of Range Binary Valuea | ||||||
| N | Percent | N | Percent | N | Percent | N | Percent |
| 4922 | 52.2 | 4505 | 47.8 | 0 | .0 | 9427 | 100.0 |
| a.” Value different from both 1 and 0”. | |||||||
| b. Binary Euclidean Distance used | |||||||
Discussion and Conclusion
Statistic aids in analysing a nation’s financial situation as well as gauging economic progress in the macro scale. Find out more Statistics, in case of micro-level, assists researchers in determining a firm’s income and profitability. In the context of a person, it includes earnings or salary, as well as other benefits. In the 1st given topic, the chosen independent variables are position, university, state and female/male, whereas in the 2nd one the independent variables are size and collaboration. The developer applied several varieties of ways to obtain all of the essential findings. The regression approach assists them in determining the VIF values, plus they can also conduct the ‘Durbin-Watson test’ evaluating university faculty members depending on genders and other variables and salary. The developers perform the ANOVA as well as cluster techniques in the second case study. These two methodologies provide students with a strong understanding of the link between inventive work or creativity as well as the scale of the organisation as well as their corporations. The developers thoroughly describe each procedure and the obtained outcomes in the assessment portion. The SPSS software is utilised by academics since it is among the most popular and well-known software packages for statistical computations. This software is very user-friendly and it produces the desired results very fast.
Reference List
Journal
Liu, Y., Zhang, S., Chen, X. and Wang, J., 2018. Artificial combined model based on hybrid nonlinear neural network models and statistics linear models—research and application for wind speed forecasting. Sustainability, 10(12), p.4601. (Liu et al.2018)
Nagy, A., Fehér, J. and Tamás, J., 2018. Wheat and maize yield forecasting for the Tisza river catchment using MODIS NDVI time series and reported crop statistics. Computers and Electronics in Agriculture, 151, pp.41-49. (Nagy et al.2018)
Sigauke, C., Nemukula, M.M. and Maposa, D., 2018. Probabilistic hourly load forecasting using additive quantile regression models. Energies, 11(9), p.2208. (Sigauke et al.2018)
Zhang, W.E., Chang, R., Zhu, M. and Zuo, J., 2022. Time Series Visualization and Forecasting from Australian Building and Construction Statistics. Applied Sciences, 12(5), p.2420. (Zhang et al.2022)
Jomnonkwao, S., Uttra, S. and Ratanavaraha, V., 2020. Forecasting road traffic deaths in Thailand: Applications of time-series, curve estimation, multiple linear regression, and path analysis models. Sustainability, 12(1), p.395. (Jomnonkwao et al.2020)
Shahoud, S., Khalloof, H., Duepmeier, C. and Hagenmeyer, V., 2020, January. Descriptive statistics time-based meta features (DSTMF) constructing a better set of meta features for model selection in energy time series forecasting. In Proceedings of the 3rd International Conference on Applications of Intelligent Systems (pp. 1-6). (Shahoud et al.2020)
Mustapa, M., Ponnusamy, R.R. and Kang, H.M., 2019. Forecasting prices of fish and vegetable using web scraped price micro data. International Journal of Recent Technology and Engineering, 7(5), pp.251-256. (Mustapa et al.2019)
Hallin, M. and Trucíos, C., 2021. Forecasting value-at-risk and expected shortfall in large portfolios: A general dynamic factor model approach. Econometrics and Statistics. (Hallin and Trucíos, 2021)
Bojer, C.S. and Meldgaard, J.P., 2021. Kaggle forecasting competitions: An overlooked learning opportunity. International Journal of Forecasting, 37(2), pp.587-603. (Bojer and Meldgaard, 2021)
Medeiros, M.C., Vasconcelos, G.F., Veiga, Á. and Zilberman, E., 2021. Forecasting inflation in a data-rich environment: the benefits of machine learning methods. Journal of Business & Economic Statistics, 39(1), pp.98-119. (Medeiros et al.2021)
Flaxman, S., Chirico, M., Pereira, P. and Loeffler, C., 2019. Scalable high-resolution forecasting of sparse spatiotemporal events with kernel methods: A winning solution to the NIJ “Real-Time Crime Forecasting Challenge”. The Annals of Applied Statistics, 13(4), pp.2564-2585. (Flaxman et al.2019)
Sulandari, W., Subanar, S., Suhartono, S., Utami, H., Lee, M.H. and Rodrigues, P.C., 2020. SSA-based hybrid forecasting models and applications. Bulletin of Electrical Engineering and Informatics, 9(5), pp.2178-2188. (Sulandari et al.2020)
Coulombe, P.G., Leroux, M., Stevanovic, D. and Surprenant, S., 2020. How is machine learning useful for macroeconomic forecasting?. arXiv preprint arXiv:2008.12477. (Coulombe et al.2020)
Dupré, A., Drobinski, P., Alonzo, B., Badosa, J., Briard, C. and Plougonven, R., 2020. Sub-hourly forecasting of wind speed and wind energy. Renewable Energy, 145, pp.2373-2379. (Dupré et al.2020)
………………………………………………………………………………………………………………………..
Know more about UniqueSubmission’s other writing services:

