Signals and Electronic Systems CIS115-6 Assignment Sample
Here’s the best sample of Signals and Electronic Systems CIS115-6 Assignment, written by the expert.
Abstract
Image compression is referred as minimizing the dimensions in terms of bytes in the file of graphics with no need of decreasing the quality of image to the level of unacceptable. This kind of decreasing the file dimensions let the storage of numerous images within the memory space and also reduces the time. There are many techniques available for image compression. The wavelet transform is very much helpful and powerful for data compressing like images. In this report we are going to design an image compression system as an element of new photography transmission system for satellite image. In this regard my task is to design algorithm for image compression using wavelet transform. Also I am going to provide the solutions for the given task. My ultimate aim is to gaining an experience in designing the system for image approximation by utilizing signal transforms.
Introduction
Generally images are consists of huge amounts of information which needs more space for storage, more bandwidth for transmission and longer duration of transmission. Hence it is benefit towards compressing the images by the process of storing the important information required to re- make the image. Analysis of wavelet is robust and supporting for this compression of information / data like images. Image like photographic compression is being done effectively by various ways. For the usage of internet there are 2 general formats of images are available such as JPEG and GIF. The method JPEG is used more frequently for the image of photograph whilst GIF is generally utilized for the images like geometrical shapes. The techniques utilized for compressing the images are wavelets and fractals.
Wavelet compression provides an access which permits to decrease the data / image size whilst, simultaneously enhancing the quality via the process of removing higher-frequency noise elements. IN this technique data / image could be decreased easily less than 1 % from its actual size. Wavelet transform is supporting image processing towards accurate analyzing the sudden changes in image which would localize the means in terms of time as well as frequency. This wavelet is exists for the duration of finite and this is having various shapes and sizes (Rao, 2015).
Literature Review
According to the author (Sulaiman Khan, 2019) , compression of images serves main role in transmission of image and storage space. This aims to decrease the dimensions of image without any remarkable loss in quality and the information in images. In order to decrease the storage space of image the author has proposed to provide compact demonstration of data in image. This compression of image is exists in the aspect of lossy or else lossless. The author has proposed a Harr Wavelet transform, DCT- discrete Cosine transforms as well running larger techniques of encoding for the latest process of manufacturing with higher rate of compression of images. This system could be implemented easily in the industries for image compression. These are then recommended for many purposes like measuring the materials for metrology in manufacturing industries, with lesser bandwidth and storage needs, also it compresses the information such as video and audio formats.
As per (V. V. Sunil Kumar, 2016), wavelet transform is utilized to feature a complicated pattern as simple series patterns as well as coefficients which, if multiplied and added, reproducing in actual pattern. There are two schemes like lossless as well as lossy compression. The later usually provides more compression compared with former. Generally wavelets are utilized to spot the prescribed signal in the domain of space as well as scaling. In this article author has created MInImage towards testing the wavelet type and functionalities are added to aid other kinds of wavelets and it utilizes the algorithm of EXW to attain good compression.
The author (Heema Sharma, 2016) states that, with the establishment of better quality image recording device it creates the images with higher resolution. However it needs large space for storage that creates the issues while transmitting as well as storing. So reduction of images is essential. Image processing is serves essential role and decreases the sizes efficiently. There exist different techniques for compression like Run Length encoding, DWT, DCT and so on. In this article, the authors have made a detailed review over the literature analysis regarding compressing images from the perception of different authors and discusses about various techniques of compression with its pros and cons.
The author, (Kamrul Hasan Talukder, 2017) explains that, with the development of technology, it is mandatory to handle huge amount of data always and it is difficult. Hence the author has proposed a less complicated two Dimension image compression techniques by using Harr wavelet towards measuring the quality of image that uses wavelets as fundamental approach. The selected wavelet technique is 2D DWT and the matrix of data / information is offered by the transform. The evaluation has been done by the factors such as ratio of compression, PSNR – Peak-signal-noise ratio, Mean score opinion, picture scale quality and more. Wavelet is applicable to images in color with 3 color elements.
Solutions
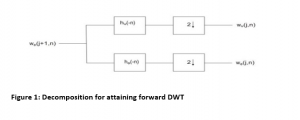
A. Forward wavelet transform with one decomposition level
For better implementation of DWT- Discrete Wavelet Transform, filter banking structure is utilized frequently. Figure exhibits the decomposition or else the filter bank analysis for attaining the forward DWT coefficients (Kehtarnavaz, 2008). The DWT of signal x[n] is depends on approximation coeff. Wɸ[j0,k] and detailed coeff. WΨ[j,k]
Where, n = 0,1,2…
J – Represents the number of levels in transform
Ψ[n] – represents wavelet functions
ɸ[n] – represents scaling function
Wavelet transform offers resolution of higher frequencies at lower frequencies as well as higher –time resolution at higher frequencies
The coefficients in high-level is passed via the filters high pass and low pass which is followed by downsampling by 2 towards computing the coefficients at bottom level, This single structure would be repeated for the decomposition for multilevel.
Recalling of wavelet transform requires to be applied with horizontal and vertical directions
The single dimensional transform could be employed to columns of horizontal transformed image
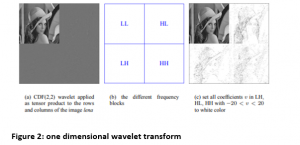
The image will be decomposed to 4 quadrants with various interpretations.
- Horizontal w ɸ h j+1
- Vertical w ɸ v j+1
LL- quadrant top left contains all coeff. That is filtered by LPF in row and then filtered with respective column. LL indicates the approximate version of actual at half of resolution
HL / LH – bottom left and top right blocks are filtered along the rows and columns with h and g by alternate. LH contains vertical edges and HL exhibits horizontal edge in clear manner
HH- bottom right quadrant derived to top left quadrant with the HPF that belongs to wavelet.
B. Reconstruction of Images with 1 synthesis level for inverse wavelet transform
Inverse DWT is got by utilizing the reconstruction or else synthesis filter bank as shown in figure 2.
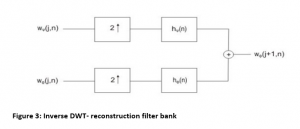
The coefficients at bottom level are being upsampled by 2 as well passed via high pass as well as low pass filter. The outcomes are being added to get the approximation values of coefficients at high-level. This is referred as mirror of computation DWT via the filter banks. DWT of signal x[n] is depends on approximation coeff. Wɸ[j,n] and detailed coeff. WΨ[j,n]
C. Deploying the wavelet transform with two iterations ( decomposition levels) to images
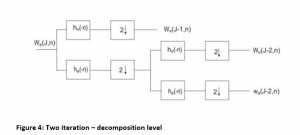
The figure shows the schematic diagram derived in A as building blocks. Computation of DWT could be iterated to attain further analysis of approximation coeffi. The blocks are h0 (n) = hɸ (-n) and h1 (n) = hΨ (-n) are called as sub band coding.
The symbol column ↓2 indicates down sampling columns by placing at even indexed column. Likewise, row ↓2 represents down sampling the rows by placing only even index rows. Column ↑2 represents upsampling by the process of inserting the zeros at odd-index column. Likewise row ↑2 indicates up-sampling of rows by inserting zeros at odd-index rows (Hlaváč, 2018)
2-D – implementation of filters via separable wavelet functions
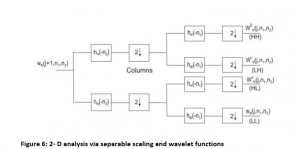
The filtering in every direction follows the sub sampling of factor 2, hence sub bands respect to filter output consists of 1/4th sample numbers compared to actual 2-D signal. The sub bands are Ψ(n1,n2),
ΨH((n1,n2), Ψv((n1,n2), and Ψd((n1,n2) these are referred to LL, LH, HL and HH respectively. 1st letter indicates low-pass else high pass filter along to the column ( vertical ) and 2nd letter indicates the low pass else high pass filtering to rows ( horizontal ).
Applying to picture

LL, LH, HL, HH sub band segments represents the approximated images and with edges of horizontal and vertical and diagonal. Decomposing the LL sub band is to have 2nd level of DWT decomposition as shown in fig. 9

D. Schematic diagram – reconstructing images – two levels
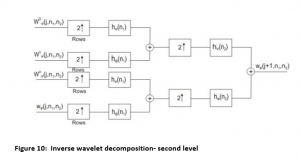
The synthesis filtering banks along rows as well as columns are related with upsampling by factor 2 hence , reconstructed image would be shown at actual resolution. Hence the filter banks are executing the IDWT and lossless as DWT.

The reconstruction is loss less ; as the coeff. of filter are indicated exactly and coeffi. are not being quantized.
E. Schematic diagram of combining C and D to apply image approximation
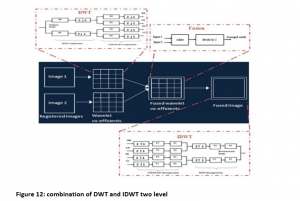
The registered images are passed as input signals via two different one-dimensional filters H0 and H1 correspondingly. H0 and H1 executes high pas and low pass filter functions for both inputs the output of every filter is sub sampling by 2 factor. The figure 12 shows the block diagram of DWT based image fusion process . the resolution for first level will be 256 x 256. IDWT utilized for computing the reconstruction of images from sub bands with less bandwidth as well slower rate of sampling. If the block is computing the IDWT transform the input , output as similar dimension as input.
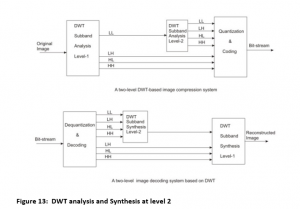
Figure 13 shows the image compression coding system supported on DWT. The coeff. are quantized and grouped in sub band over the subband relies on coding system. This shows decoding process also to get the reconstructed image.
F. Number of operations required for forward, reverse wavelet transform
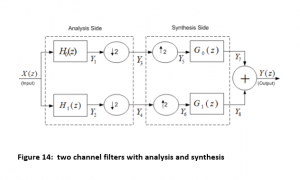
H0 (z) – LPF Discrete analysis with angular frequency π /2
H1 (z) – HPF- discrete analysis with angular frequency π /2
G0 (z) – LPF synthesis with angular frequency π /2
G1 (z) – LPF synthesis with angular frequency π /2
Down sampler
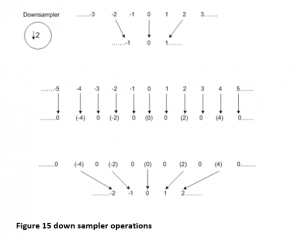
The sequence numbers indicates the samples of images . this can be look into 2 steps as shown in figure. The symbol (-) indicates the samples that are retained with no kill and no braces indicates with kill -samples . then the last image shows the compression.
Upsampler

This is invert to down sampler functions. This is called as expander (V.M.Gadre, 2016). The number of operations for forward and reverse is 6
For the image having pixels are 1024 x 1024 are also being upsampling and down sampling like above process.
G. Matlab coding
For calculating the Mean square error
Err = immse ( X,Y)
This calculates the means-squared error between the arrays x and y.
Ref = imread ( ‘pout, tif);
Imshow(ref)

Mean – squared error betwixt two images
err= immmse( A, ref);
fprintf(‘/n The mean- squared error is % 0.4 f/n’,err);
The mean – squared error will be 353.76 (Mathworks, 2021)
Likewise we need to calculate the image from Breo.
clear
clc
im=imread(‘image in Breo’);
im=im1 single(im);
h1=1/9*ones(3,3);
imf1=imfilter(im,h1,’replicate’);
h2=1/25*ones(5,5);
%
MSE=mean(mean((im-imf1).^2));
MaxI=1;% the maximum possible pixel value of the images.
PSNR =10*log10((MaxI^2)/MSE);
Conclusion
The functions of discrete wavelet and Inverse discrete wavelet for image compression at single decomposition , and two iterations of decomposition level and combination of DWT and IDWT with image approximation and calculating the number of operations needed for image approximation is calculated and then matlab code for calculating the mean square value of the image obtained from Breo site. Thus we have completed the assignment as per the requirement
References
Heema Sharma, P. S. D., 2016. Image Compression Using Wavelet Transform: A Literature. International Journal of Engineering Research and General Science, 4(6), pp. 188-200.
Hlaváč, V., 2018. Wavelets transformation, s.l.: http://people.ciirc.cvut.cz/~hlavac/TeachPresEn/11ImageProc/14WaveletsEn.pdf.
Kamrul Hasan Talukder, a. K. H., 2017. Haar Wavelet Based Approach for Image Compression. IAENG International Journal of Applied Mathematics, 36(1), pp. 1-8.
Kehtarnavaz, N., 2008. Digital signal Processign Ssytem Design. Second ed. s.l.:https://www.sciencedirect.com/topics/computer-science/wavelet-transforms.
Kharagpur, v. 2.-. I., 2017. Multi-Resolution Analysis, s.l.: https://nptel.ac.in/content/storage2/courses/117105083/pdf/ssg_m4l12.pdf.
Mathworks, 2021. Mean- squared error, s.l.: https://www.mathworks.com/help/images/ref/immse.html.
Rao, N., 2015. How will wavelet transforms be useful for image processing ?. Research Gate, Volume 3, pp. 1-7.
Sulaiman Khan, s. N. A. H. e., 2019. An efficient JPEG image compression based on Haar wavelet transform, discrete cosine transform, and run length encoding techniques for advanced manufacturing processes. Sage Journals, 52(9), pp. 1532-1544.
V. Sunil Kumar, M. I. S. R., 2016. Image Compression Techniques by using Wavelet Transform. Journal of Information Engineering and Applications, 2(5), pp. 1-6.
V.M.Gadre, 2016. WAVELETS AND MULTIRATE DIGITAL SIGNAL PROCESSING. DSP, 6(https://nptel.ac.in/content/storage2/courses/117101001/downloads/Lec-10_Script.pdf), pp. 1-7.
________________________________________________________________________________
Know more about UniqueSubmission’s other writing services:

