BEST STATISTICS FOR BUSINESS DECISIONS
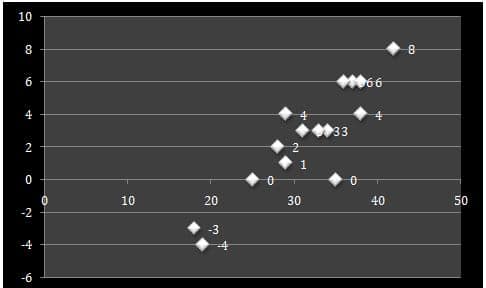
In this case, the relation between the television and weight of the children is presented in a scatter plot.
As mentioned by Ly et al. (2018), this describes that as the data that are gathered are closely related to each other. As a result of that, the data are not scattered from each other, which describe the data are closely linked with each other. [Referred to Appendix 1]
The value of r determines the Pearson’s coefficient that is Pearson’s r. According to Armstrong (2019), the value of r varies from +1 to -1.
In this case, it is evident that the value is equal to 0.89. Besides that evaluation of r determines the slope of the regression line of the data that are gathered. As mentioned by Obilor and Amadi (2018) that the value is nearly equal to +1, this signifies that the slope is positive and closely related to each other.
Hence here, the argument is the amount of television reduces the time for physical exercise and leads to overweight of the child. [Referred to Appendix 2]
Thus from the value with an enhancement in time of watching television, the amount of overweight among the children is increasing.
The value of r is equal to 0.89, which signifies that the slope of the regression line is positive, and the value also shows positive relationships among the variables.
The regression line allows the researcher to determine the relationship between the variables. As mentioned by Downar and Duivesteijn (2017), it describes the link between the number of hours spent in front of the TV and the overweight of children.
As mentioned by Eslami et al. (2018), in analysing the relationship between the TV and overweight, it is observed that the value of the intercept is positive and the value of the coefficient is also positive. Besides that from the r-value, it is clear that slope will be positive, and they will possess a positive relationship between them.
Similarly, the value of the intercept is 26.71, and the slope of the regression line will be equal to 1.82. Hence, from the regression line, it is observed that the link between hours spent in front of the TV and overweight is positively related to each other. [Referred to Appendix 3]
The regression line can be written as:
Y= 26.71+ 1.82X
d) Coefficient of determination
The coefficient of the determination determines the degree of correlation among the dependent and independent variables that are considered for the analysis.
As mentioned by Eslami and Saeed (2018), this value also varies from +1 to -1. In addition, if the evolution of the coefficient is more than 0.5, then it will possess a strong positive correlation. As mentioned by Shafi et al. (2016), if the evaluation is greater than -0.5, this will signify that it will possess strong positive correlation among them.
On the other hand, this situation can affect the relationship between the variables. The value is greater than 0.5, and the evaluation is equal to 0.79. This value signifies that the value is positively correlated with each other, and it represents that with an enhancement in the number of hours, the overweight of the children will rise.
Besides that, it can be represented that the value of the regression coefficient is positive, and as the slope is positive, this will signify that the regression line will be rising upwards.
In analysing the data, it is observed that if children spend 42 hours in front of the television, then it will result in 8kg of overweight. Hence, with an enhancement in the television hours, the overweight of the children will rise.
Therefore the values among the variables are positive and strongly correlated to each other. In analysing the relationship between the TV and overweight, it is observed that the value of the intercept is positive and the value of the coefficient is also positive.
The significance value of the data represents the chance that the hypothesis is accepted. Besides that, the value is useful in determining the significance of the value that will be gathered from the calculation.
According to Downar and Duivesteijn (2017), the level of significance is at 5%. This represents that with an enhancement in the evaluation, the significance of the data that is gathered will rise.
In this perspective, the value of significance is considered as 0.05. Therefore, the evaluation is (p<0.05); this signifies that the value is significant to each other. Hence, with a change in the deviation of the value, the hypothesis can be rejected.
In this appearance, it will signify that if the time changes in front of the television can reduce the overweight of the children. In case children spend 19 hours in front of the television, then it will not lead to any overweight.
Besides that, with an augmentation of the value, the overweight of children also augment. Hence, with an enhancement in the television hours, the overweight of the children will rise.
Therefore the values among the variables are positive and strongly correlated to each other. In analysing the relationship between the TV and overweight, it is observed that the value of the intercept is positive and the value of the coefficient is also positive.
The standard error value of the variable signifies the accuracy of the value. The enhancement in the evaluation of standard error reduces the accuracy of the evaluation. The values of the standard error are 3.26.
As mentioned by Shafi et al. (2016), hence the value is not greater than 5, which signifies that an augmentation in evolution can affect the fit of the regression model. In case the value is less than five then it will signify that the regression line is the best fit line in this model.
Besides that, it determines the accuracy of the model that is it allows determining the accuracy of the relationship between the variables. It is observed that the value is less than five, and it is the best fit line which allows determining the degree of relationship. Hence, the regression model is the best fit model in this case.
Armstrong, R.A., 2019. Should Pearson’s correlation coefficient be avoided?. Ophthalmic and Physiological Optics, 39(5), pp.316-327.
Downar, L. and Duivesteijn, W., 2017. Exceptionally monotone models—the rank correlation model class for exceptional model mining. Knowledge and Information Systems, 51(2), pp.369-394.
Eslami, T. and Saeed, F., 2018. Fast-gpu-pcc: A gpu-based technique to compute pairwise pearson’s correlation coefficients for time series data—fmri study. High-throughput, 7(2), p.11.
Eslami, T., Awan, M.G. and Saeed, F., 2017, August. GPU-PCC: A GPU Based Technique to Compute Pairwise Pearson’s Correlation Coefficients for Big fMRI Data. In Proceedings of the 8th ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics (pp. 723-728).
Ly, A., Marsman, M. and Wagenmakers, E.J., 2018. Analytic posteriors for Pearson’s correlation coefficient. Statistica Neerlandica, 72(1), pp.4-13.
Obilor, E.I. and Amadi, E.C., 2018. Test for Significance of Pearson’s Correlation Coefficient. International Journal of Innovative Mathematics, Statistics & Energy Policies, 6(1), pp.11-23.
Shafi, J., Waheed, A. and Sanober, S., 2016. Dependency Test: Portraying Pearson’s Correlation Coefficient Targeting Activities in Project Scheduling. International Journal of Advanced Computer Science and Applications, 7(9), pp.351-356.
(Source: Created by learner)
| Television (hours) | Overweight(Kg) | ||
| Television (hours) | 1 | ||
| Overweight(Kg) | 0.89119 | 1 | |
(Source: Created by learner)
| SUMMARY OUTPUT | ||||||||
| 26 | ||||||||
| Multiple R | 0.89119 | |||||||
| R Square | 0.79422 | |||||||
| Adjusted R Square | 0.778391 | |||||||
| Standard Error | 3.260832 | |||||||
| Observations | 15 | |||||||
| ANOVA | ||||||||
| df | SS | MS | F | Significance F | ||||
| Regression | 1 | 533.504 | 533.504 | 50.17425 | 8.25E-06 | |||
| Residual | 13 | 138.2293 | 10.63302 | |||||
| Total | 14 | 671.7333 | ||||||
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | Lower 95.0% | Upper 95.0% | |
| Intercept | 26.71303 | 1.07668 | 24.81056 | 2.47E-12 | 24.38701 | 29.03906 | 24.38701 | 29.03906 |
| X Variable 1 | 1.828321 | 0.258114 | 7.083378 | 8.25E-06 | 1.270699 | 2.385943 | 1.270699 | 2.385943 |
(Source: Created by learner)


